L'épreuve de mathématiques du BAC S a suivi nombre de modes depuis bientôt 10 ans que je la suis.
Il y a eu la mode QCM
(2004-2005), puis la mode ROC
(2006), puis la mode "question ouverte"...
Nous sommes clairement aujourd'hui dans la mode algorithmique, d'une popularité sans précédent puisque s'étendant même au delà de la série S
(séries ES, L et bientôt technologiques), et même au-delà du BAC!
En effet, un exercice d'algorithmique vient de tomber au Concours Général de Mathématiques 2013.
Le voici:
Nous nous devons donc d'aider Sisyphe, qui avance à partir de la case '0' avec un dé à 6 faces, et se doit d'atteindre ou dépasser 100 tout en évitant les nombres premiers.
Mais il n'y a que 25 nombres premiers inférieurs à 100 - un jeu d'enfant me direz-vous?
Approchons le problème de façon empirique à l'aide d'une petite simulation.
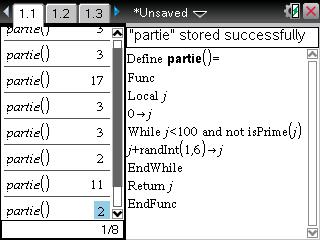
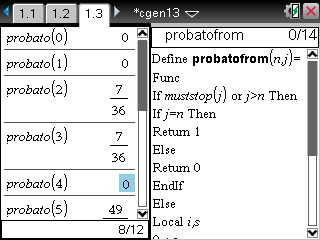
Voici un programme TI-Nspire qui renvoi le numéro de la case sur laquelle Sisyphe termine sa partie, c'est-à-dire:
- un nombre supérieur ou égal à 100 si il gagne
- un nombre premier inférieur à 100 si il perd
Comme vous voyez, j'ai effectué 8 parties et ai toujours perdu en atteignant un nombre premier inférieur à 100...
Mais peut-être est-ce de la malchance? Il faut simuler un grand nombre de parties pour que la fréquence d'apparition d'un événement tende vers sa probabilité.
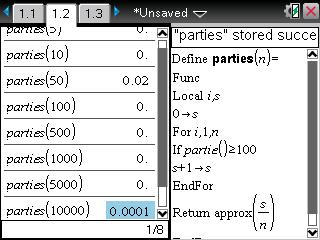
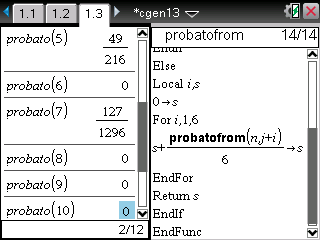
Voici un autre programme TI-Nspire destiné à nous renvoyer la fréquence des parties gagnantes pour une simulation de n parties:
La probabilité de gagner la partie est effectivement très faible... Malgré plusieurs centaines ou milliers de parties simulées, la fréquence des parties gagnantes en souvent nulle ou très proche de zéro...
Les apparences sont donc trompeuses, et ce pauvre Sisyphe porte donc bien son nom, tel son homologue mythologique père d'Ulysse, qui fut damné à pousser un rocher jusqu'en haut d'une colline, ce rocher ayant une très forte probabilité de redégringoler alors immédiatement puisqu'il s'agit d'un équilibre instable
(dérivée seconde du potentiel négative).
Bon, venons-en enfin aux questions qui nous intéressent.
Dans la 2ème partie, on étudie la loi de probabilité de variable aléatoire X, où X prend pour valeurs le numéro de la case en fin de partie
(qu'elle soit gagnée ou perdue).
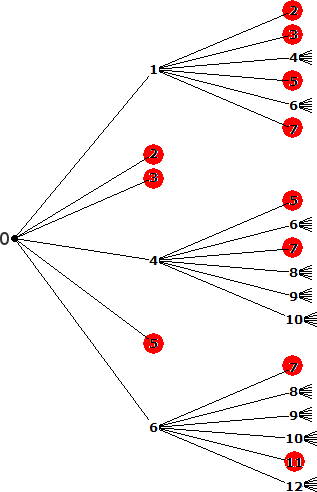
Les événements X=2 et X=3 sont aisément dénombrables via un arbre.
On code ici en rouge l'événement
"atteindre un nombre premier inférieur à 100", ce qui met fin à la partie.
A partir de la case 0, on peut atteindre la case 2 en:
- sortant directement 2 (probabilité 1/6)
- sortant 1 puis 1 (probabilité 1/36)
Donc P(X=2)=7/36.
La case 2 étant interdite
(nombre premier), les seules façons d'atteindre 3 sont en:
- sortant directement 3 (probabilité 1/6)
- sortant 1 puis 2 (case intermédiaire: 1 - probabilité 1/36)
Donc encore P(X=3)=7/36.
Les cases 2 et 3 étant interdites
(nombres premiers), les seules façons d'atteindre 5 sont en:
- sortant directement 5 (probabilité 1/6)
- sortant 4 puis 1 (case intermédiaire: 4 - probabilité 1/36)
- sortant 1 puis 4 (case intermédiaire: 1 - probabilité 1/36)
- sortant 1 puis 3 puis 1 (cases intermédiaires: 1, 4 - probabilité 1/216)
Donc P(X=5)=49/216.
Les nombres 0, 1 et 4 étant des nombres non premiers ils ne peuvent achever une partie et on a donc de façon triviale P(X=0)=P(X=1)=P(X=4)=0.
On en déduit que P(X>=4)=1-P(X<4)=1-(P(X=0)+P(X=1)+P(X=2)+P(X=3))=11/18
Mais nous aurons bien évidemment beaucoup de mal à esquisser un arbre qui va plus loin...
La question nous demande donc en conséquence la production d'un algorithme permettant de déterminer P(X=k).
En utilisant les formules de probabilités d'événements successifs indépendants, on peut construire un algorithme récursif qui va parcourir l'arbre en profondeur, chaque nouvelle sous-branche correspondant à une multiplication par 1/6.
Nous allons utiliser pour cela sur TI-Nspire:
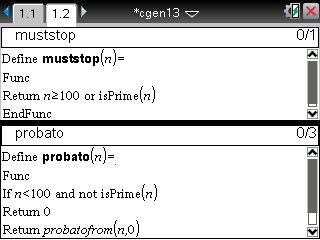
- une fonction testant si le noeud de l'arbre est un noeud arrêtant la partie
- une fonction pour initialiser la récursivité
Et il nous faut enfin la fonction récursive en tant que telle, qui à partir d'un noeud-parent se réappelle sur les 6 noeuds-fils
(dé tiré entre 1 et 6) pour calculer les probabilités par multiplication par 1/6 et somme.
Cette fonction travaille donc branche par branche.
Elle renverra 0 si on termine la partie sans atteindre le nombre cherché, ce qui par produit annulera les chemins inutiles ici et permettra de ne considérer par somme que les 'bons' chemins.
Il ne s'agit probablement pas de l'algorithme le plus rapide, et une version itérative serait sans doute plus performante.
Mais je trouvais la version récursive plus naturelle à comprendre.
Dans tous les cas, il s'agit probablement d'un problème de complexité exponentielle, et quoi que l'on fasse l'algorithme explosera donc rapidement les capacités de toutes les machines actuelles.
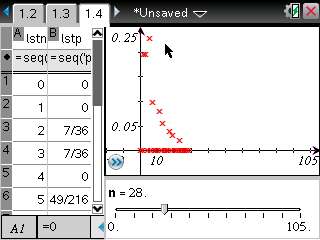
Sur TI-Nspire notamment, en partant de P(X=0) on passe de calculs instantanés à des calculs de quelques secondes, puis quelques minutes, et enfin quelques heures sur P(X=29).
Tout juste peut-on conjecturer que la suite des P(X=k) non nuls semble décroissante à partir du rang 5 et tendre rapidement vers 0.
D'ici à ce qu'elle arrive à P(X=105), l'univers a certainement le temps de s'écrouler...
Edit: Pour une version itérative de l'algorithme, voir les commentaires de la news.Rappelons que si les nombres premiers et plus généralement l'arithmétique, l'algorithmique et la programmation t'intéressent, nous tenons encore pour deux semaines un concours sur les nombres premiers-palindromes! Liens:Sujet du Concours Général de Mathématiques 2013Document TI-Nspire support pour l'exercice 3
by 
), l'utilisation de cet OS vaudra peut être mieux que l'utilisation d'un OS de TI qui est assez mal conçu sur la 84+C avec des laps de temps beaucoup trop longs, et c'est d'autant plus vrai qu'un moteur CAS est prévu pour cet OS. 
