Aujourd'hui le bêta-test de la future mise à jour
Epsilon 24 franchit une nouvelle étape avec la disponibilité de la version
24.2.2.
Chez
NumWorks, nous allions vers trois ans de mises à jour inhabituellement rares et relativement mineures de la calculatrice graphique, la dernière évolution majeure étant l'ajout de l'application de tableau périodique des éléments en 2022. Nous nous demandions sur quoi le constructeur pouvait bien travailler depuis, et nous avions plusieurs hypothèses, comme une
calculatrice scientifique pour le Collège ou encore la refonte ô combien nécessaire de la plateforme en ligne.
Le bêta-test d'
Epsilon 24 nous apporte une réponse partielle à cette interrogation, même si cela amène d'autres questions.

4 versions bêta ont été disponibles à ce jour :
- 24.0.0 le 11 décembre 2024
- 24.0.1 dès le 12 décembre 2024
- 24.2.0 le 3 juillet 2025
- 24.2.2 le 7 juillet 2025
Le test d'aujourd'hui concerne donc cette dernière version
24.2.2.
Découvrons ensemble les changements.
A1) Calculatrices graphiques et calcul exactGo to top Les calculatrices graphiques de milieu de gamme disposent d'un moteur de calcul exact. À la place d'écritures décimales éventuellement approchées, ce dernier permet d'obtenir les résultats numériques sous la forme exacte attendue par l'enseignant de Mathématiques.
Sur les modèles milieu de gamme de
Casio (Graph 35+E II, Graph 90+E, Graph Math+) et
Texas Instruments (TI-82 Advanced Edition Python, TI-83 Premium CE Edition Python), le moteur en question est de type
QPiRac. C'est-à-dire qu'il se base sur des propriétés remarquables
(notamment sur les parties décimales) pour identifier et afficher correctement les nombres appartenant aux 2 familles suivantes :
Ces familles sont également gérées par la calculatrice
NumWorks, positionnée elle aussi dans le milieu de gamme de par son prix :
Ces deux familles étaient adaptées à l'ancien programme de Première Scientifique jusqu'à l'année scolaire 2018-2019.
Il est à noter que ce n'est hélas plus le cas de nos jours. Depuis l'année scolaire 2019-2020, les exponentielles sont abordées en spécialité Mathématiques dès la classe de Première Générale.
Heureusement nous avons la
NumWorks qui fait mieux. En effet le fonctionnement de son moteur de calcul exact
Poincaré est différent ; il travaille non pas en faisant tourner des algorithmes numériques sur les résultats approchés, mais directement sur des arbres de calculs permettant de représenter les différentes saisies.
Là où la concurrence se contente d'écritures décimales approchées dès que l'on sort des deux familles précédentes, la
NumWorks à la différence a l'immense avantage d'être capable de retourner une valeur exacte pour n'importe quelle saisie algébrique ! 👍
A2) Calculatrices NumWorks et calcul littéralGo to top 

À l'origine la
NumWorks était même encore plus géniale que cela. Le moteur faisant appel non pas à des algorithmes numériques mais à des algorithmes de traitement d'arbres, les noeuds pouvaient être aussi bien des valeurs numériques que des lettres ou expressions littérales. Il était ainsi possible de saisir des expressions littérales et d'en obtenir une simplification en résultat
(développement + réduction) ! 👍
Cette fonctionnalité rajoutée dès
décembre 2017 avec la mise à jour
1.2 du
firmware officiel
Epsilon fut malheureusement désactivée en
juin 2019 avec la mise à jour
11.2,
NumWorks estimant qu'elle constituait un obstacle à ses projets d'expansion à l'international, nombre de nos voisins européens interdisant en effet déjà toute fonctionnalité de calcul littéral ou formel à leurs examens de l'enseignement secondaire.

Toutefois le fonctionnement interne de
Poincaré n'a pas changé. Les arbres continuent à pouvoir mélanger noeuds numériques et littéraux, et le moteur continue à procéder aux simplifications par développements et réductions. C'est juste à la fin si l'expression correspondant à l'arbre obtenu après traitement fait encore appel à des termes littéraux, que le résultat affiché est au dernier moment remplacé par la valeur
undef.
Pour ceux qui disposent d'une calculatrice
NumWorks N0100 (arrêtée pour la rentrée 2019) ou
N0110 (arrêtée pour la rentrée 2023), il est ainsi possible de réactiver le calcul littéral en installant un
firmware Omega ou
Upsilon. Ces
firmwares tiers sont des
forks améliorés du
firmware officiel
Epsilon, et entre autres retirant justement la limitation précédente.

Et précisons de plus qu'avec la mise à jour
Epsilon 15.3 de
janvier 2021,
NumWorks avait changé son algorithme de détermination de nombres dérivés. L'algorithme numérique pouvant retourner des résultats faux dans bien des cas particuliers avait été remplacé par une véritable dérivation de l'expression de la fonction au niveau de l'arbre de calcul, autrement plus fiable.
Les
firmwares tiers
Omega et
Upsilon exploitent fort avantageusement ce nouvel algorithme, en te permettant d'obtenir l'expression littérale de la fonction dérivée ! 👍
Pour cela, dans ta saisie demandant le nombre dérivé en une valeur, il suffit de remplacer la valeur en question par la variable de la fonction.
Si à la différence tu disposes d'une calculatrice plus récente
NumWorks N0115 ou
N0120 à ce jour incompatible avec les
firmwares non officiels, pas de dérivation littérale possible.
Mais concernant les développement et réduction d'expressions littérales il y a toutefois une astuce si tu sais faire preuve d'un minimum de malice.

Si ton expression ne fait intervenir au maximum que 3 paramètres, il te suffit de remplacer chaque paramètre de l'expression par une des 3 constantes numériques suivantes qui à la différence sont parfaitement autorisées à intervenir dans les arbres-résultats :
π,
e et
i. La seule chose à laquelle il faut faire attention lors de ce choix, c'est à ce qu'aucune des propriétés spécifiques à la constante en question n'intervienne lors de la simplification de l'expression.
Exemple : pour développer et réduire
$mathjax$(a-2)^3$mathjax$
, il suffit par exemple d'associer la constante
π au paramètre
a. La saisie de
$mathjax$(π-2)^3$mathjax$
nous permettra d'obtenir après un tout petit effort de renommage que l'expression développée est
$mathjax$a^{3}-6a^{2}+12a-8$mathjax$
! 👍
Nous évoquerons par la suite l'utilisation de cette astuce en tant que
pseudo-calcul littéral.


Lors de notre
test de la version bêta précédente
24.0.1, nous t'annoncions un tout nouveau moteur de calcul. Nous remarquions une différence de signature trigonométrique.
Nous bénéficions d'améliorations de certains résultats, comme par exemple les sommes acceptant un nombre plus important de termes, permettent de meilleures études des séries numériques :
Très clairement,
NumWorks était en train d'effectuer une réécriture intégrale du moteur de calcul
Poincaré...
À l'époque de la version bêta
24.0.1 de
décembre 2024, ce nouveau moteur de calcul était manifestement défectueux.
Diverses formes de résultats n'étaient plus simplifiées correctement :
C'était encore pire dans le cas de résultats complexes avec des formes d'écritures non respectées ou même des résultats totalement inutiles :
Le moteur de calcul
Poincaré étant sollicité de façon transversale par les diverses applications, les conséquences étaient loin de se limiter à la seule application
Calculs :
Face à l'ampleur sans précédent de ces régressions, dans l'intérêt des élèves, nous formions des vœux pour qu'
Epsilon 24 ne sorte pas avant les examens 2025.
Mais ce n'était pas tout. Il y avait également de quoi profondément attrister les plus grands fans de
NumWorks, avec
Epsilon 24.0 le pseudo-calcul littéral ne fonctionnait plus du tout :
NumWorks a donc fait le choix de la prudence en nous sortant cette nouvelle version bêta d'
Epsilon 24 après la session d'examens 2025.
Et bien la version bêta
Epsilon 24.2 semble corriger l'ensemble des dysfonctionnements précédents.
Par rapport à l'édition précédente
Epsilon 23, nous remarquons au passage la notation désormais naturelle des écritures décimales utilisant des puissances de 10, en lieu et place de l'opérateur infixé
E hérité des premières calculatrices scientifiques utilisant des afficheurs à 7 segments.
Quelques anomalies persistent toutefois, comme ici l'absence surprenante de la forme exacte du résultat pour les factorielles de 16, 17 et 18... comportement difficilement compréhensible alors que le résultat exact plus grand est à nouveau communiqué à partir de la factorielle de 19.
Toutefois autre excellente nouvelle qui devrait en ravir plus d'un, le peuso-calcul littéral est cette fois-ci de retour ! 👍
Investir autant de temps, d'énergie et donc d'argent dans la réécriture d'un moteur de calcul qui est déjà, comme nous avons vu, le meilleur de tout le milieu de gamme... L'objectif visé n'est pas évident, mais doit clairement en valoir la peine. Cette réécriture est l'arbre qui cachait la forêt, il y a quelque chose de majeur qui se prépare, et nous ne savons pas encore exactement quoi.
La
version française du
changelog parle d'un moteur de calcul plus souple et plus puissant, permettant une meilleure exactitude des résultats et ainsi qu'une meilleure gestion d'objets mathématiques comme les unités :
NumWorks wrote:Pour cette version, nous avons modifié en profondeur notre moteur de maths, pour le rendre plus souple et plus puissant. La conséquence est une plus grande exactitude dans nos calculs et des objets mathématiques mieux gérés. Par exemple, un gros travail a été fait pour améliorer la gestion des unités.
Nous doutons toutefois que cela suffise à justifier un tel investissement, soudainement 7 ans après la sortie de la calculatrice, alors que rien ne faisait de l'ombre au moteur
Poincaré si ce n'étaient les modèles formels proposés par la concurrence, mais dans le créneau du haut de gamme et donc plus chers.
La
version anglaise est un peu plus disserte à ce sujet, évoquant un changement pour faciliter des évolutions futures :
NumWorks wrote:In this software version, we've extensively modified our math engine, making it more flexible and powerful. The result is greater accuracy in our calculations and better management of mathematical objects. Many of these features will be undetectable, but are essential to long term growth of our software.
As a result of this improvement, you may notice increased input size of complex calculations involving matrices, increased accuracy of logarithmic functions where the result is a fractional value, and that outputs including units of measurement will better match user expectations (including operations with science constants).
Il y a donc bel et bien anguille sous roche,
NumWorks nous prépare quelque chose qui méritait un tel investissement, et donc quelque chose de majeur ! Reste maintenant à savoir quoi...
B) Onglets Graphique (Grapheur, Suites, Régression)Go to top Evoquons l'onglet
Graphique disponible dans les applications
Grapheur,
Suite et
Régression.
Il te donne accès à la représentation graphique dans un repère des données saisies.
Et bien nouveauté attendue depuis des années, comme chez la concurrence il devient enfin possible de régler la graduation des axes. Mais mieux encore qu'un simple rattrapage de la concurrence, le réglage accepte les valeurs non entières, qui sont ensuite affichées en étiquettes des axes sous forme exacte, une fonctionnalité qui n'était présente jusqu'ici que sur le haut de gamme
TI-Nspire.
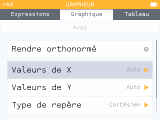

En conséquence un confort exceptionnel dans le cadre par exemple de représentations graphiques de fonctions trigonométriques :
C) Application Grapheur et fonctionsGo to top Afin de faciliter et d'accélérer tes études de fonctions, la
NumWorks avait déjà le gros avantage de t'identifier les points remarquables sur leurs graphes.
Epsilon 24 apporte deux types d'améliorations significatives à ce sujet :
- davantage de points remarquables sont identifiés et te sont désormais présentés (discontinuités, intersections avec les frontières de représentations graphiques d'inéquations, …)
- et surtout, amélioration majeure dans le respect des codes Mathématiques, il y a désormais une distinction visuelle entre les points remarquables appartenant au graphe et ceux n'y appartenant pas !
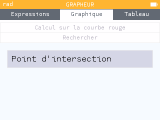

Afin de sélectionner rapidement et précisément un point d'intersection sans avoir à aller le chercher en déplaçant le curseur à l'aide des touches fléchées, tu pouvais appeler le menu contextuel sur la vue graphique avec
OK
puis sélectionner
Rechercher. Ton curseur était alors positionné exactement sur un point d'intersection, et dans le cas où il y en avait plusieurs, les touches fléchées te permettaient d'alterner directement entre les différents points d'intersection.
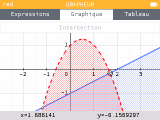

Nouveauté, découlant de ce qui précède, ce menu est dorénavant également fonctionnel dans le cadre de représentations graphiques d'inéquations !
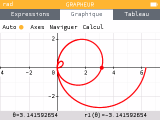

Enfin, dans le cadre de représentation graphique de fonctions polaires, le menu contextual via la touche
OK
te permet désormais de consulter les coordonnées cartésiennes en plus des coordonnées polaires !
Dans le cadre de suites définies par récurrence, l'application
Suites bénéficie d'une nouvelle interface de saisie dans le respect des notations Mathématiques :
E) Onglets Données (Statistiques, Régression)Go to top L'onglet
Données permettant la saisie dans les applications
Statistiques et
Régression bénéficie d'une amélioration significative.
Tu pouvais jusqu'ici y saisir un maximum de 3 séries statistiques. Désormais, tu pourras travailler simultanément sur un maximum de 6 séries statistiques !
La calculatrice NumWorks disposait d'un gros défaut - l'intégralité des données mémoire était définitivement perdue lors de l'utilisation du mode examen.
Tu perdais donc entre autres tout ce que tu avais pu mettre dans ta calculatrice (scripts Python, applications, ...), et ici de façon définitive. Il te fallait tout réinstaller manuellement après chaque utilisation du mode examen, à condition bien sûr d'avoir accès à une copie (attention donc aux scripts Python saisis directement sur la calculatrice).
C'était d'autant plus incompréhensible qu'il n'y avait pas ce problème chez la concurrence. Depuis une décennie, les données préexistantes y étaient juste verrouillées lors de l'activation du mode examen (c'est-à-dire rendues inaccessibles) puis.
Avec
Epsilon 24,
NumWorks s'attaque enfin à ce problème et annonce enfin, la récupération des données préchargées lors de la désactivation du mode examen !
Les données ainsi récupérables sont les scripts
Python, expressions, fonctions, listes, équations.
Attention toutefois aux
NumWorks bien pleines, la priorité étant donnée au bon fonctionnement de la calcualtrice en mode examen. Dans les cas où le volume de données saisies en mode examen excède la capacité de stockage de ta mémoire
RAM, la sauvegarde de tes données préchargées sera automatiquement supprimée dans son intégralité pour faire de la place. Et dans ce cas, tu ne retrouveras pas tes données lors de la désactivation du mode examen.
NumWorks semble toutefois s'être montré très timide sur cette fonctionnalité, qui est hélas loin d'atteindre le niveau de la concurrence.
Précisons en effet que la sauvegarde lors de l'activation du mode examen ne concerne que les données que tu as préchargées en mémoire
RAM.
Elle ne concerne malheureusement pas ce que tu as pu mettre en mémoire
Flash, notamment les applications que tu as installées.

C'est même pire que cela, si tu as installé la moindre application additionnelle en mémoire
Flash, cette fonctionnalité de sauvegarde et restauration des données de la mémoire
RAM sera complètement court-circuitée, car dans ce cas la calculatrice démarre le mode examen en effectuant un redémarrage. À l'activation du mode examen, tu perdras ainsi non seulement l'ensemble des applications installées en mémoire
Flash, mais également l'intégralité des données de ta mémoire
RAM.
Avoir enfin accédé aux souhaits de la minorité vocale des utilisateurs mettant des scripts Python sur leur calculatrice et ayant envie d'en conserver certains sans avoir à la réinstaller à chaque utilisation du mode examen est une bonne chose.
Mais fort malheureusement, cela a été codé au détriment de la majorité silencieuse des utilisateurs scolaires.
Rappelons en effet qu'une des choses ayant toujours été présentée comme la plus urgente à faire en fin d'épreuve, c'est de désactiver le mode examen. Parce qu'il entraîne une surconsommation de piles/batterie avec le clignotement de la diode empêchant l'extinction complète de la calculatrice, et parce qu'il faut arriver à l'éventuelle prochaine épreuve avec un mode examen désactivé. Comme cette désactivation ne peut se faire de manière autonome et nécessite du matériel externe, il est essentiel de l'effectuer dès que l'on a le bon matériel sous la main.
Or désormais, à la désactivation du mode examen, tu perds l'intégralité des données saisies pendant le mode examen. Cela implique que tu perds certes les éventuels petits scripts Python créés pendant ton épreuve, mais aussi les fonctions définies, les séries statistiques saisies, ou encore l'historique des calculs effectués. Tu perds donc toute trace de ton travail pendant l'examen, ce qui t'empêchera donc de le confronter correctement aux corrigés qui sortent dès la fin de l'épreuve.
Rappelons que jusqu'à la version précédente Epsilon 23, la calculatrice NumWorks conservait bien les données saisies en mode examen. C'est également le cas d'autres modèles populaires comme la bien moins chère TI-82 Advanced Edition Python ou encore la populaire TI-83 Premium CE. C'était un gros avantage notamment par rapport aux calculatrices Casio.
Si on fait le bilan, cette nouveauté n'est donc pas une amélioration mais une régression. Espérons donc que NumWorks acceptera de corriger cela d'ici la version stable, dans l'intérêt supérieur de la masse des utilisateurs scolaires.


L'application
Paramètres t'offre une nouvelle option :
Mise en veille.
Elle te permet dès maintenant de choisir le délai d'inutilisation au bout duquel la calculatrice réduit l'éclairage de l'écran, afin d'économiser la batterie.
Ce délai est toujours de 30 secondes par défaut, mais si cela ne convient pas à ton usage il t'est possible désormais d'opter pour 1, 2 ou même 5 minutes.


Lorsque tu branchais ta
NumWorks sur un hôte USB actif
(ordinateur, tablette, smartphone, ...) tu bénéficiais d'un écran explicatif dédié au transfert de données.
Toutefois, rien de tel lorsque tu branchais ta calculatrice à un hôte USB passif
(adaptateur secteur, batterie USB, ...). La recharge n'était que très discrètement indiquée par l'icône de batterie en haut à droite de l'écran.


Dorénavant avec
Epsilon 24, dans le cas d'un branchement pour recharge tu bénéficies ici aussi d'un écran explicatif dédié, t'expliquant entre autres qu'une charge complète nécessite 6 heures.
Ajoutons de plus à cela des messages d'alerte lorsque ta batterie chute sous les 20% de charge.

 Pour la rentrée 2023, des escrocs avaient mis un ligne une imitation de la boutique distributeur scolaire Calcuso, proposant la seule calculatrice NumWorks au prix anormalement bas de 59,99€.
Pour la rentrée 2023, des escrocs avaient mis un ligne une imitation de la boutique distributeur scolaire Calcuso, proposant la seule calculatrice NumWorks au prix anormalement bas de 59,99€.
 Attention à toi car l'arnaque est de retour pour cette rentrée 2025.
Attention à toi car l'arnaque est de retour pour cette rentrée 2025. La calculatrice NumWorks y est proposée à seulement 59,99€, qui plus est accompagnée de la housse Wyngs comme chez Calcuso, accessoire jusqu'ici jamais proposé chez NumWorks. Une promotion extrême temporaire (expire dans moins de 3 jours pour te pousser à un achat non réfléchi) qui n'a aucun sens quand on connaît le succès croissant de NumWorks mais également en cette période (début du mois d'août).
La calculatrice NumWorks y est proposée à seulement 59,99€, qui plus est accompagnée de la housse Wyngs comme chez Calcuso, accessoire jusqu'ici jamais proposé chez NumWorks. Une promotion extrême temporaire (expire dans moins de 3 jours pour te pousser à un achat non réfléchi) qui n'a aucun sens quand on connaît le succès croissant de NumWorks mais également en cette période (début du mois d'août). Lancé apparemment le 7 août soit il y a seulement 4 jours et bien qu'annonçant livrer en 3 à 5 jours, le faux site NumWorks prétend déjà satisfait plus de 640 commandes. C'est à la fois trop pour un site créé il y a 4 jours, et trop peu quand on prétend se faire passer pour le site NumWorks créé en 2017 et cumulant sans doute au moins des centaines de milliers de ventes si ce ne sont des millions.
Lancé apparemment le 7 août soit il y a seulement 4 jours et bien qu'annonçant livrer en 3 à 5 jours, le faux site NumWorks prétend déjà satisfait plus de 640 commandes. C'est à la fois trop pour un site créé il y a 4 jours, et trop peu quand on prétend se faire passer pour le site NumWorks créé en 2017 et cumulant sans doute au moins des centaines de milliers de ventes si ce ne sont des millions.
 Si la page d'accueil tente de te faire croire que tu es bien chez NumWorks, les pages de contact et mentions légales terminent de te révéler l'arnaque, en te donnant une adresse courriel en gmail.com et un numéro de portable, révélant au passage que ce n'est pas la boutique officielle NumWorks mais une toute autre boutique Shopify.
Si la page d'accueil tente de te faire croire que tu es bien chez NumWorks, les pages de contact et mentions légales terminent de te révéler l'arnaque, en te donnant une adresse courriel en gmail.com et un numéro de portable, révélant au passage que ce n'est pas la boutique officielle NumWorks mais une toute autre boutique Shopify.

























































































