Pour la rentrée 2024, Casio sort une nouvelle calculatrice graphique couleur, la Graph Math+ Lycée, en remplacement de sa Graph 90+E de rentrée 2017.
Nous avons aujourd'hui le plaisir de pouvoir t'en faire une première présentation détaillée, car Casio vient tout juste de publier son manuel.
De quoi récupérer davantage d'informations sur les innovations du logiciel... et peut-être même déduire quelques caractéristiques du matériel. C'est parti !
De quoi récupérer davantage d'informations sur les innovations du logiciel... et peut-être même déduire quelques caractéristiques du matériel. C'est parti !
- Emballage et alimentation
- Système d'exploitation
- Boîtier et clavier
- Menu d'accueil : Applications disponibles et définition écran
- Point sur les applications manquantes
- Connectivité et port USB-C
- Esprit de la nouvelle interface
- Application Calculs
- Menu Catalogue, conversions d'unités et préfixes SI
- Menu Variables
- Application Stats
- Application Probabilités
- Application Graphe&Table et zone graphique
- Application Python, zone graphique écran et getkey()
- Application Equations
- Application Suites
- Application Paramètres
- Application Mode examen et définition complète écran
- Application Base-N
- Application Mémoire : Capacités, formats de fichiers supportés et point sur les applications additionnelles
- Echantillons et émulateurs
- Conclusion
1) Emballage et alimentationGo to top
C'est clairement confirmé par le manuel, alimentation par 4 piles AAA :
Ce n'est pas forcément un point faible ; tout est question de point de vue. Nos tests montrent qu'à matériel et donc consommation similaire, l'autonomie de bonnes piles AAA est nettement supérieure à celles des batteries Lithium-ion que les concurrents préinstallent dans leurs modèles, et ce même en testant contre des batteries neuves complètement chargées.
Mais après si tu y tiens, rien ne t'empêche d'utiliser des piles AAA rechargeables, une pratique officiellement supportée et même encouragée par Casio, comme nous verrons plus loin dans l'application Paramètres.
2) Système d'exploitationGo to top
Le titre du manuel nous indique ici que les calculatrices Graph Math+ commercialisées seront préchargées en usine avec un système en version 1.00.
- pour la Graph 90+E c'est CY-811AY
- pour son équivalent fx-CG50AU en Australie c'est CY-810FY
- pour son équivalent fx-CG50 dans le reste du monde c'est CY-810AY
Et bien la référence du logiciel de la Graph Math+ nous est connue, mentionnée sans doute involontairement dans les noms de fichiers de plusieurs visuels publiés sur le site de Casio. Ce sera CY-875A.
Impossible en l'état toutefois de déduire quelque chose sur le matériel à partir de ça, la numérotation étant loin d'être toujours consécutive.
Cette numérotation commune à tous les modèles graphiques est en effet croissante dans le temps, entre nous avons eu des CY-835 à CY-838 pour la génération monochrome USB Power Graphic 3 à partir de la rentrée 2019 (dont en France les Graph 25+E II et Graph 35+E II).
Elle est toutefois loin d'être consécutive pour des raisons que nous ignorons encore. Il serait possible que les dictionnaires électroniques Casio qui utilisent la même plateforme matérielle que les graphiques couleur mais que nous connaissons hélas encore bien trop peu partagent la même numérotation et expliquent ces sauts.
3) Boîtier et ClavierGo to top
Le clavier Graph Math+ change complètement de celui de la Graph 90+E pour reprendre la nouvelle organisation introduite avec les Casio scientifiques de génération CW Classwiz depuis la rentrée 2022, ce qui inclut entre autres la fx-92 Collège Classwiz de rentrée 2023 ou la Graph Light Lycée de rentrée 2024.
C'est-à-dire notamment que l'on y dispose :
- d'une touche
CATALOG
donnant accès par catégories à l'ensemble des fonctions transversales intégrées à la calculatrice - d'une touche
...
amenant à un menu contextuel listant les fonctions ou opérations spécifiques à l'application courante - une touche
VARIABLE
ouvrant un gestionnaire de variables - 2 touches fléchées haut/bas supplémentaire pour défiler les menus directement d'un écran complet vers le haut ou vers le bas, similaires aux touches page précédente/suivante d'un clavier d'ordinateur
- une touche
SETTINGS
pour les réglages
D'une part, nous avons des différences communes aux Graph Math+ et Graph Light :
- mise en valeur de la fonction secondaire d'extinction OFF sur la touche
AC
- le séparateur décimal passe de la virgule au point, et la touche
,
est donc remplacée par.
- par conséquent le séparateur d'arguments passant du point virgule à la virgule
- la touche
;
n'est donc plus nécessaire et est remplacée par l'exponentielle indispensable au lycée, avec les logarithmes rajoutés en fonctions secondaires sur les emplacements vides de la même rangée de touches du clavier - la touche
Rép
permettant d'invoquer le dernier résultat disparaît, cédant la place à,
pour le séparateur d'arguments - l'invocation du dernier résultat est déplacée en fonction secondaire de la touche
FORMAT
- nombre complexe i accessible en fonction secondaire de la touche
9
Déjà, les inscriptions clavier sont ici en Anglais. Au vu des habitudes de Casio avec les modèles précédents, cela suggère qu'à la différence des fx-92 Collège Classwiz et Graph Light, la Graph Math+ disposera d'un modèle équivalent hors de France. La fx-CG50, équivalent international à la Graph 90+E française, bénéficiera donc d'un sucesseur, peut-être fx-CG60, fx-CG80 ou fx-CG100, mais probablement pas avant la rentrée 2025 vu l'absence totale du moindre indice à ce sujet à ce jour.
Même nombre de touches au clavier, aussi la touche transversale
f(x)pour le gestionnaire de définitions de fonctions disparaît, au profit du retour du modificateur
ALPHAavec ici un accès intégral à l'alphabet.
Les touches de fonction
F1à
F6de la Graph 90+E sont supprimées. 2 touches fléchées supplémentaires sont ici rajoutées pour les remplacer. Ces onglets sont donc désormais purement logiciels, les 2 touches en question permettant juste d'activer l'onglet précédent ou suivant. Plusieurs avantages significatifs en conséquence pour l'intuitivité :
- déjà comme déjà dit nous ne sommes plus limités à 1/6 de l'écran pour la largeur d'un onglet, ce qui permet enfin de limiter ou supprimer complètement l'utilisation d'abréviations pas toujours heureuses pour les élèves en étiquette de chaque onglet ! 👍
- mais aussi, les instructions ou tutoriels d'enseignants n'utiliseront plus de noms de touches F1-F6 mais à la place les noms des onglets à activer, ce qui d'une part donnera ici encore davantage de sens à chaque manipulation, et d'autre part restera valide en cas d'une mise à jour changeant l'ordre de certains de ces onglets ! 👍
Pour le reste :
- La division euclidienne en fonction secondaire de la touche
÷
disparaît ici - Plusieurs fonctions secondaires caractéristiques de la Graph 90+E sont reprises ici sur la rangée inférieure du clavier, mais cette fois-ci indiquées avec des icônes plutôt que des inscriptions : capture d'écran, sélection, copier-coller
4) Menu d'accueil : Applications disponibles et définition écranGo to top
Le manuel est déjà l'occasion pour nous de récupérer nos toute premières captures d'écran Graph Math+ à l'échelle 1:1. Nous comptons 384×216 pixels, ce qui certes légèrement moins que les 396×224 pixels de la Graph 90+E, mais il ne faut pas oublier que l'écran de cette dernière présentait des marges réservées à l'indication de la configuration du mode examen via un remplissage selon différentes couleurs, et que ces marges sont justement ignorées par certains des outils de capture d'écran de Casio. Donc très probablement, nous restons avec la Graph Math+ sur le même écran en 396×224 pixels.
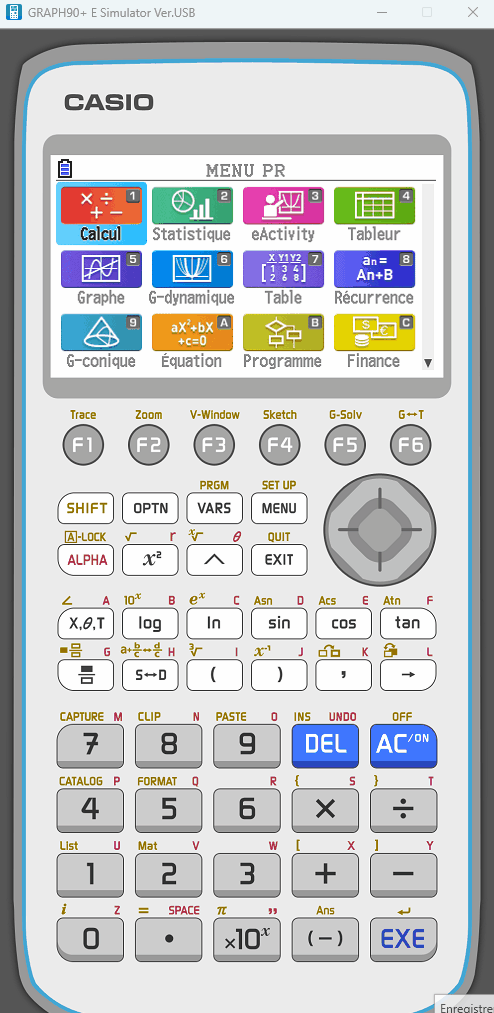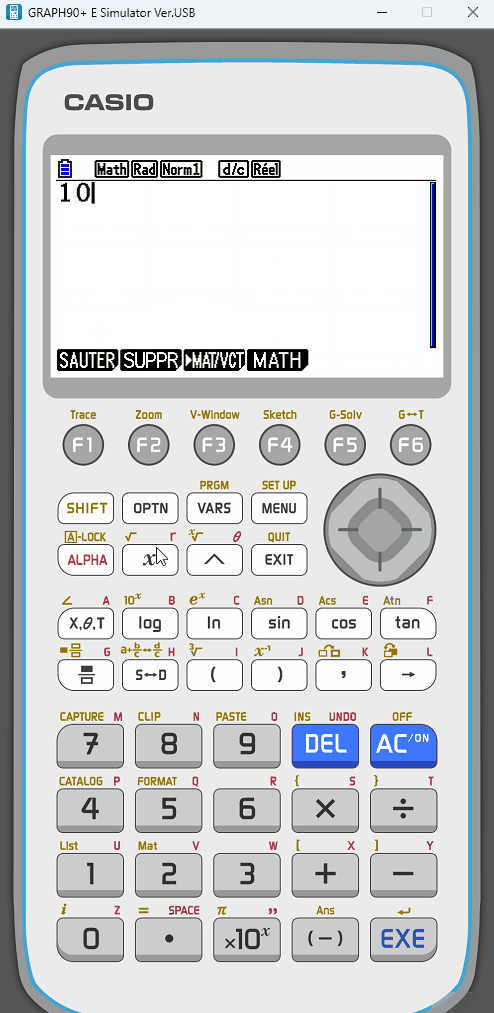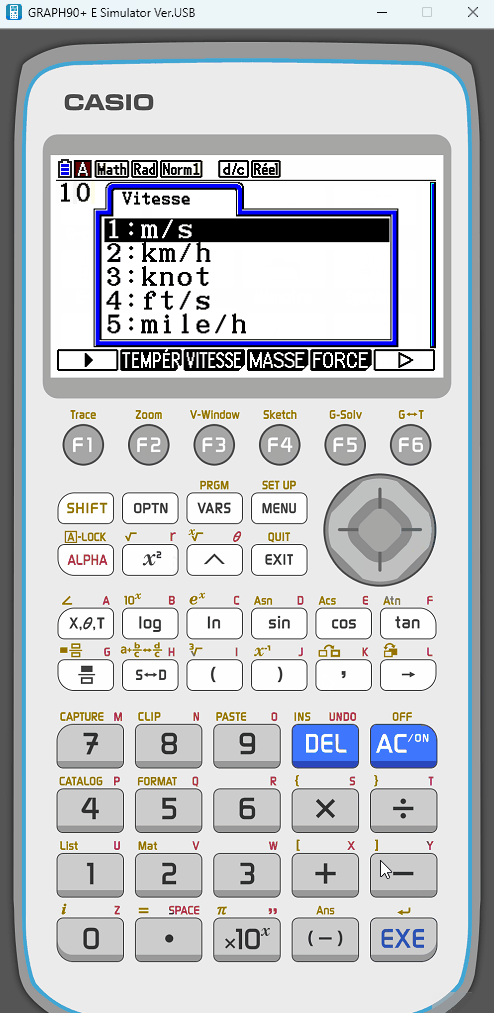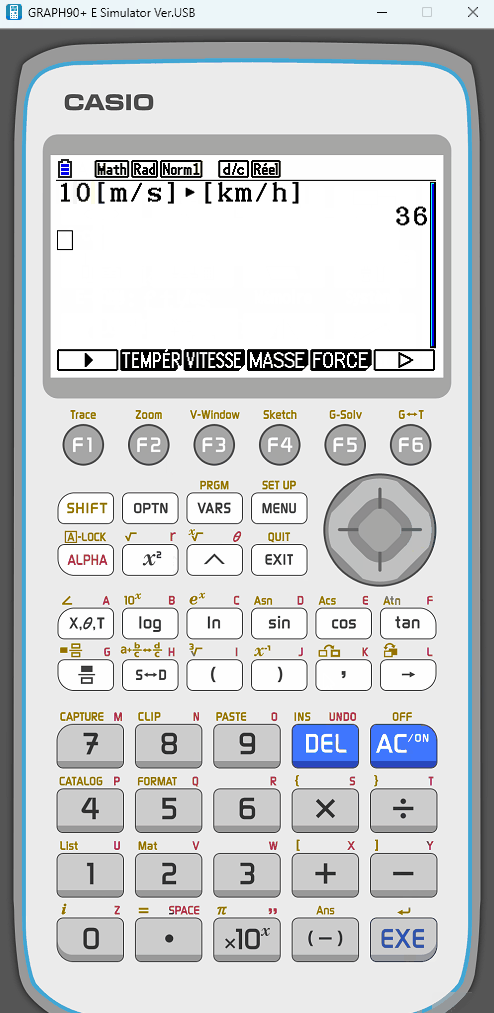
Ceci étant dit, première impression par rapport à la Graph 90+E, Casio semble ici avoir fait le choix d'un design autrement plus épuré pour la Graph Math+. L'écran d'accueil ci-contre met en effet beaucoup moins en avant les capacités couleur de l'écran, se contentant d'afficher les icônes d'applications en 4 teintes (du noir, du blanc, des variantes de rouge, des variantes de bleu). Cela rappelle d'ailleurs très fortement les fx-92 Collège Classwiz et Graph Light, qui utilisaient 4 niveaux de gris pour les icônes d'applications sur ce même écran (noir, blanc, gris clair, gris foncé).
Regardons maintenant rapidement ce qui est disponible niveau applications. Quelques changements ou ajouts :
- Sur la Graph 90+E, les représentations graphiques de fonctions et tableaux de valeurs de fonctions étaient disponibles dans 2 applications distinctes, Graphe et Table. Si elles partageaient fort heureusement les mêmes définitions de fonction, il n'en restait pas moins qu'il fallait donc régulièrement changer d'application alors que l'on continuait pourtant à travailler sur les mêmes données.
Avec la Graph Math+ c'est fini, ces fonctionnalités étant regroupées au sein d'une même application Graph&Table ! 👍 - Une toute nouvelle application Base-N dédiée aux calculs dans différentes bases numériques ! 👍
- L'application Système semble pour sa part renommée en Paramètres.
- Une toute nouvelle application Mode examen 👍
5) Point sur les applications manquantesGo to top
Si tu as bien compté jusqu'ici, en fait il nous manque pas mal d'applications au menu principal.
Là où la Graph 90+E présente de 19 à 24 applications (selon si l'on compte ou pas les applications additionnelles officielles préinstallées en usine en plus des applications intégrées), la Graph Math+ ne présenterait donc que plus 11 applications à ce jour.
Si la réduction s'explique en petite partie par des fusions d'applications (comme par exemple Graphe et Table qui deviennent Graphe&Table), c'est très loin de justifier un tel écart.
Nous nous inquiétions donc également de plusieurs manques. Aucune trace, du moins sur l'écran d'accueil Graph Math+ précédent, de fonctionnalités Graph 90+E plus ou moins importantes.
Déjà il manquerait, a priori, toutes les fonctionnalités offertes sur Graph 90+E via les applications additionnelles officielles préinstallées en usine :
Mais nous notons également des absences remarquées par rapport aux applications intégrées sur Graph 90+E :
Casio a communiqué là-dessus.
Déjà un équivalent à l'application Finance est bien déjà disponible quelque part, sous la forme d'un menu. Peut-être donc une entrée dans le menu contextuel (touche
Sur le reste, Casio nous annonce une mise à jour majeure (peut-être donc déjà une version 2.00) en cours de développement pour la rentrée 2025. Cette mise à jour rajoutera :
Là où la Graph 90+E présente de 19 à 24 applications (selon si l'on compte ou pas les applications additionnelles officielles préinstallées en usine en plus des applications intégrées), la Graph Math+ ne présenterait donc que plus 11 applications à ce jour.
Si la réduction s'explique en petite partie par des fusions d'applications (comme par exemple Graphe et Table qui deviennent Graphe&Table), c'est très loin de justifier un tel écart.
Nous nous inquiétions donc également de plusieurs manques. Aucune trace, du moins sur l'écran d'accueil Graph Math+ précédent, de fonctionnalités Graph 90+E plus ou moins importantes.
Déjà il manquerait, a priori, toutes les fonctionnalités offertes sur Graph 90+E via les applications additionnelles officielles préinstallées en usine :
- application Physium pour le tableau périodique des éléments chimiques et la bibliothèque de constantes physiques
- application Graphe 3D pour les représentations dans un repère 3D de différents types d'objets (droite, plan, sphère, cylindre, cône)
- application Sim prob pour le simulateur d'expériences aléatoires
- application Géométrie pour la géométrie dynamique
- application Plot Image pour la superposition de tracés de graphes sur une image
Mais nous notons également des absences remarquées par rapport aux applications intégrées sur Graph 90+E :
- application Tableur pour les feuilles de calcul
- application Programme pour l'édition et utilisation de programmes dans le langage interprété historique Casio Basic
- application G-dynamique pour l'animation des graphes de fonctions paramétrées
- application G-conique pour les représentations graphiques de fonctions coniques
- application Lien pour le transfert de données entre calculatrices
- application eActivity pour l'édition de documents scientifiques
- application E-CON4 pour l'acquisition de mesures physiques
- application Finance pour les calculs financiers
Casio a communiqué là-dessus.
Déjà un équivalent à l'application Finance est bien déjà disponible quelque part, sous la forme d'un menu. Peut-être donc une entrée dans le menu contextuel (touche
...) d'une des applications, ou bien une entrée au catalogue (touche
CATALOG).
Sur le reste, Casio nous annonce une mise à jour majeure (peut-être donc déjà une version 2.00) en cours de développement pour la rentrée 2025. Cette mise à jour rajoutera :
- des fonctionnalités équivalentes aux applications Graph 90+E intégrées Tableur, G-dynamique et G-conique
- des fonctionnalités équivalentes aux applications additionnelles Graph 90+E préinstallées (Physium, Graphe 3D, Sim Prob et Géométrie)
- applications intégrées Programme, Lien, eActivity et E-CON4
- application additionnelle Plot Image
- eActivity qui peut être vu comme un éditeur d'anti-sèches (bien que permettant bien mieux que cela) et rencontrer donc une certaine hostilité de la part d'enseignants ou institutions, notamment lorsqu'il n'y a pas de mise en place systématique du mode examen (évaluations en classe, examens internationaux, autres pays vu que la Graph Math+ semble comme nous avons vu ne pas avoir été développée spécifiquement pour la France, etc.)
- l'application Programme puisque le langage Casio Basic n'est plus utilisé au lycée français - peut-être sera-t-elle à la différence toujours présente dans le système d'exploitation équipant les successeurs des fx-CG50
6) Connectivité et port USB-CGo to top
Niveau connectivité nous avons une excellente nouvelle à t'apprendre. La Graph Math+ abandonne enfin le port mini-USB pour lequel les élèves et enseignants avaient de moins en moins souvent la bonne connectique sous la main en cas de besoin, au profit d'un port USB-C ! 👍
Le port série historique mini-Jack 2.5mm est pour sa part conservé.
Si nous avons bien lu et compris, les câbles USB et mini-Jack ne seront plus fournis avec la calculatrice ; peut-être un moyen pour Casio de faire un effort sur le prix en faveur des utilisateurs en cette période de forte inflation.
Niveau USB cela ne devrait pas être bien gênant, les utilisateurs n'auront qu'à essayer les câbles USB-C qu'ils auront sous la main, et juste mettre de côté ceux qui ne fonctionneront pas pour la connectivité (c'est-à-dire ceux qui ne sont pas complets car juste câblés pour la recharge inutile ici).
Il restera toutefois possible d'acquérir auprès des distributeurs Casio un pack de connectivité SB-2000 comprenant 1 câble USB-C complet et 1 câble mini-Jack 2.5mm (SB-62).
Par contre, nous venons de voir que les applications de connectivité Graph 90+E (Lien pour la communication avec une autre calculatrice et E-CON4 pour la communication avec une interface d'acquisition de données physiques) n'étaient plus présentes.
On aurait certes pu imaginer une ouverture automatique d'une interface dédiée dès que l'on connecte la Graph Math+ à une autre calculatrice ou bien à l'interface d'acquisition CMA CLAB, comme c'est déjà le cas lors d'une connexion de la calculatrice à un ordinateur ou encore à un vidéoprojecteur Casio.
Sauf que nous avons parcouru le manuel et ces cas de connexion ne sont même plus évoqués. La Graph Math+ ne semblerait donc plus disposer de capacités de communication avec une deuxième calculatrice, l'interface d'acquisition CMA CLAB, ou même les vidéoprojecteurs de marque Casio (ce dernier point étant moins surprenant, la branche vidéoprojecteurs de Casio ayant été fermée en 2021).
À ce jour, le port série mini-Jack 2.5mm ne semblerait donc plus servir qu'à une seule et unique chose : la désactivation du mode examen d'une deuxième calculatrice. Ce serait assez étrange de l'avoir conservé juste pour ça, dans le sens non optimal niveau coût d'assemblage de chaque machine. Le port USB aurait parfaitement pu être utilisé à cette fin, comme chez la concurrence.
Le port série historique mini-Jack 2.5mm est pour sa part conservé.
Si nous avons bien lu et compris, les câbles USB et mini-Jack ne seront plus fournis avec la calculatrice ; peut-être un moyen pour Casio de faire un effort sur le prix en faveur des utilisateurs en cette période de forte inflation.
Niveau USB cela ne devrait pas être bien gênant, les utilisateurs n'auront qu'à essayer les câbles USB-C qu'ils auront sous la main, et juste mettre de côté ceux qui ne fonctionneront pas pour la connectivité (c'est-à-dire ceux qui ne sont pas complets car juste câblés pour la recharge inutile ici).
Il restera toutefois possible d'acquérir auprès des distributeurs Casio un pack de connectivité SB-2000 comprenant 1 câble USB-C complet et 1 câble mini-Jack 2.5mm (SB-62).
Par contre, nous venons de voir que les applications de connectivité Graph 90+E (Lien pour la communication avec une autre calculatrice et E-CON4 pour la communication avec une interface d'acquisition de données physiques) n'étaient plus présentes.
On aurait certes pu imaginer une ouverture automatique d'une interface dédiée dès que l'on connecte la Graph Math+ à une autre calculatrice ou bien à l'interface d'acquisition CMA CLAB, comme c'est déjà le cas lors d'une connexion de la calculatrice à un ordinateur ou encore à un vidéoprojecteur Casio.
Sauf que nous avons parcouru le manuel et ces cas de connexion ne sont même plus évoqués. La Graph Math+ ne semblerait donc plus disposer de capacités de communication avec une deuxième calculatrice, l'interface d'acquisition CMA CLAB, ou même les vidéoprojecteurs de marque Casio (ce dernier point étant moins surprenant, la branche vidéoprojecteurs de Casio ayant été fermée en 2021).
À ce jour, le port série mini-Jack 2.5mm ne semblerait donc plus servir qu'à une seule et unique chose : la désactivation du mode examen d'une deuxième calculatrice. Ce serait assez étrange de l'avoir conservé juste pour ça, dans le sens non optimal niveau coût d'assemblage de chaque machine. Le port USB aurait parfaitement pu être utilisé à cette fin, comme chez la concurrence.
7) Esprit de la nouvelle interfaceGo to top
L'interface Graph 90+E n'était en fait qu'une version colorisée et agrandie de celle de la Graph 35+E II. On retrouvait très exactement les mêmes écrans et menus. Pour remplir cet objectif la Graph 90+E utilisait une police de caractères ridiculement grosse, lui permettant de faire rentrer à l'écran très exactement les mêmes nombres de lignes et colonnes de caractères. Un choix qui très clairement avait fort tristement bridé tout ce qu'il était possible de faire avec la formidable définition en 396×224 pixels de l'écran.
Avant d'explorer plus en détails certaines de ces applications, nous allons te présenter en quelques mots l'esprit de la nouvelle interface Graph Math+, et ce afin que tu remarques encore mieux les changements dans ce qui va suivre.
Avec la Graph Math+ nous partons littéralement vers de tout nouveaux horizons. C'est ici toute l'interface qui a été repensée, ne ressemblant a priori à rien de connu, et il est maintenant grand temps de la découvrir.
 Un changement concerne donc les onglets de bas d'écran, avec toujours 2 onglets affichés même si davantage peuvent être disponibles. Cela permet d'avoir beaucoup plus de place pour les décrire explicitement, plus besoin d'abréviations !
Un changement concerne donc les onglets de bas d'écran, avec toujours 2 onglets affichés même si davantage peuvent être disponibles. Cela permet d'avoir beaucoup plus de place pour les décrire explicitement, plus besoin d'abréviations !
Mais avant d'aller plus loin nous nous devons de te préciser quelque chose d'essentiel ; ces onglets n'ont apparemment plus rien à voir avec ce que tu as connu sur les graphiques Casio depuis le siècle dernier. Avec la Graph Math+ il y a en effet un radical changement radical de philosophie à leur sujet.
Sur Graph 90+E, les onglets de bas d'écran servaient à saisir/déclencher des actions, éventuellement en passant par des sous-menus d'onglets. Sur Graph Math+ à la différence, ils sont exclusivement dédiés à basculer entre différentes vues (on pourrait dire aussi écrans ou pages) de l'application courante. Un changement hautement pertinent permettant aux élèves de mieux acquérir la compétence Représenter !
Quant aux actions, puisqu'elles semblent désormais totalement absentes des onglets de bas d'écran il faut bien les mettre quelque part. Nous avons à cette fin des boutons dédiés aux actions qui apparaissent au sein même des interfaces des différentes vues.
L'interface a également tendance à laisser autant que possible visible le contexte d'appel, notamment par :
Un avantage scolaire est donc de ne plus couper brutalement et totalement l'utilisateur du contexte d'appel par des affichages plein écran dans ces cas-là, le contexte restant donc (partiellement) visible à l'écran ! 👍
Nous allons de suite t'illustrer ce que donne tout ceci en prenant en exemple plusieurs des applications intégrées. Et cela va être également l'occasion de voir que Casio est très loin de s'être contenté des ces aspects transversaux, mais a également fait des choses spécifiques au moins pour certaines de ces applications.
Avec la Graph Math+ nous partons littéralement vers de tout nouveaux horizons. C'est ici toute l'interface qui a été repensée, ne ressemblant a priori à rien de connu, et il est maintenant grand temps de la découvrir.
Mais avant d'aller plus loin nous nous devons de te préciser quelque chose d'essentiel ; ces onglets n'ont apparemment plus rien à voir avec ce que tu as connu sur les graphiques Casio depuis le siècle dernier. Avec la Graph Math+ il y a en effet un radical changement radical de philosophie à leur sujet.
Sur Graph 90+E, les onglets de bas d'écran servaient à saisir/déclencher des actions, éventuellement en passant par des sous-menus d'onglets. Sur Graph Math+ à la différence, ils sont exclusivement dédiés à basculer entre différentes vues (on pourrait dire aussi écrans ou pages) de l'application courante. Un changement hautement pertinent permettant aux élèves de mieux acquérir la compétence Représenter !
Quant aux actions, puisqu'elles semblent désormais totalement absentes des onglets de bas d'écran il faut bien les mettre quelque part. Nous avons à cette fin des boutons dédiés aux actions qui apparaissent au sein même des interfaces des différentes vues.
L'interface a également tendance à laisser autant que possible visible le contexte d'appel, notamment par :
- la superposition d'une ou même plusieurs fenêtres popup pour les appels d'interfaces, menus ou saisies, en lieu et place d'un affichage plein écran
- une aide en ligne discrète dans la barre de titre
- la table des caractères spéciaux dont l'interface lorsque appelée prend la place des onglets de bas d'écran, au lieu ici encore d'un affichage plein écran
- des icônes flottantes notifiant certains événements
Un avantage scolaire est donc de ne plus couper brutalement et totalement l'utilisateur du contexte d'appel par des affichages plein écran dans ces cas-là, le contexte restant donc (partiellement) visible à l'écran ! 👍
Nous allons de suite t'illustrer ce que donne tout ceci en prenant en exemple plusieurs des applications intégrées. Et cela va être également l'occasion de voir que Casio est très loin de s'être contenté des ces aspects transversaux, mais a également fait des choses spécifiques au moins pour certaines de ces applications.
8) Application CalculsGo to top
L'onglet Calcul te permet une saisie en écriture naturelle, et gère différents types de calculs :
Losqu'un résultat matriciel, vectoriel ou sous forme de liste devient trop grand (plus de 256 octets), il s'ouvre en détails dans une fenêtre Rep et est ensuite indiqué sous forme abrégée dans l'historique de calculs. L'affichage détaillée peut être réobtenu à tout moment en sélectionnant le résultat dans l'historique des calculs et tapant
- calcul numérique
- calcul complexe / imaginaire
- calcul vectoriel
- calcul matriciel
- calculs sur des listes que nous évoquerons plus loin
- calcul exact QPiRac pour les éléments réels des types précédents rentrant dans les 2 familles de nombres suivantes :
- QPi : multiples rationnels de π - $mathjax$\pm\frac{a\pi}{b}$mathjax$(pour les angles en radians notamment)
- QRac : binômes de rationnels et/ou radicaux - $mathjax$\frac{\pm a\sqrt{b} \pm c\sqrt{d}}{f}$mathjax$(ce qui couvre un large ensemble allant des fractions du collège aux racines de polynômes du 2nd degré au lycée en passant par nombre de valeurs remarquables en trigonométrie)
- QPi : multiples rationnels de π -
OK.
Losqu'un résultat matriciel, vectoriel ou sous forme de liste devient trop grand (plus de 256 octets), il s'ouvre en détails dans une fenêtre Rep et est ensuite indiqué sous forme abrégée dans l'historique de calculs. L'affichage détaillée peut être réobtenu à tout moment en sélectionnant le résultat dans l'historique des calculs et tapant
OK.
EXITcomme sur Graph 90+E !
26 vecteurs nommés de Vct A à Vct Z peuvent être affectés ou consultés directement dans cet onglet, auxquels s'ajoute le vecteur Vct Ans associé au dernier résultat vectoriel.
La dimension de chaque vecteur peut aller jusqu'à 999.
Ici aussi 26 matrices nommées de Mat A à Mat Z peuvent être affectés ou consultés dans cet onglet, auxquels s'ajoute la matrice Mat Ans associée au dernier résultat matriciel.
Chaque matrice peut avoir jusqu'à 999 lignes et 999 colonnes.
9) Menu Catalogue, conversions d'unités et préfixes SIGo to top
CATALOGpermet d'invoquer pour tes saisies un menu transversal. Il s'agit d'un catalogue énumérant l'ensemble des fonctions intégrées à la calculatrice. C'est maintenant la touche essentielle pour ces saisies, nombre de fonctions n'étant plus directement accessibles au clavier dans le cadre de la simplification de ce dernier.
Précisons que les fonctions que nous allons présenter ici seront disponibles pour les saisies effectuées dans l'ensemble des applications de la calculatrice, aussi bien l'application Calculs que nous venons de couvrir que les autres applications que nous allons te présenter, à l'exception de la seule application Python qui dispose d'un catalogue spécifique.
Les fonctions sont dont ici listées sous plusieurs entrées au catalogue.
L'entrée Tout te permet d'accéder à l'ensemble des fonctions intégrées de façon alphabétique ; tu choisis d'abord la première lettre pour te voir alors présenter les fonctions associées par ordre alphabétique :
La sous-entrée Symboles est dédiée à l'ensemble fonctions ou opérateurs alphabétiques.
Il t'y est même possible à l'aide du menu contextuel via la touche
...d'y épingler la saisie sélectionnée afin qu'elle ne disparaissant pas de l'historique suite à tes prochaines saisies et y soit conservée. Très pratique pour des saisies que tu effectuerais régulièrement ! 👍
- Etude de fonction : dérivées, intégrale, maximum et minimum locaux d'une fonction, opérateur de sommation (Σ), logarithmes, solveur, division euclidienne, simplification
- Probabilités : factorielle, fonctions de dénombrement, fonctions aléatoires
- Calcul numérique : pgcd, ppcm, valeur absolue, parties entière et fractionnaire, arrondis, reste division euclidienne, ...
- Conversion d'unités : permet de convertir une unité dans une autre unité de même type, une superbe fonctionnalité pour les Mathématiques et surtour les sciences expérimentations (Physique-Chimie).
On distingue pour chaque type de conversion possible :- 18 unités de longueur
- 9 unités d'aire
- 15 unités de volume
- 4 unités de température
- 5 unités de vitesse
- 10 unités de masse
- 5 unités de force
- 10 unités de pression
- 14 unités d'énergie
- 5 unités de puissance
- Données variables : accès aux variables système, c'est-à-dire des variables préexistantes n'ayant pas été créées par l'utilisateur et reprenant les paramètres de configuration ou résultats de diverses applications (paramètres statistiques, configurations de tableau de valeurs de suites ou fonctions, configuration de fenêtre graphique, etc.)
- Vecteur : pour la saisie des 27 noms de vecteurs possibles et leurs fonctions de calcul associées (produits scalaire et vectoriel, angle entre 2 vecteurs, vecteur unitaire, norme)
- Matrice : pour la saisie des 27 noms de matrices possibles et leurs fonctions de calcul associées (déterminant, inverse, transposée, matrice identité, remplissage, dimension, ...)
- Nombre complexe : pour la saisie du nombre imaginaire i et des fonctions de calcul associées (module, argument, conjugué, parties réelle et imaginaire, conversion entre formes algébrique et polaire)
- Statistiques : pour la saisie des 27 noms de listes et leurs fonctions de calcul associées (permet d'utiliser sous la forme d'une saisie dans un champ de calcul, les fonctionnalités offertes par l'interface de l'application Statistiques que nous allons couvrir plus loin)
- Angle/Coord/Sexa : pour les conversions d'angles en degrés, radians ou grades et les fonctions de calcul associées
- Lois de probabilités : permet d'utiliser sous la forme d'une saisie dans un champ de calcul, les fonctionnalités offertes par l'interface de l'application Probabilités que nous allons couvrir plus loin)
- Fonction hyperbolique : accès aux fonctions de trigonométrie hyperbolique et à leurs fonctions inverses
- Préfixes d'unités : pour les saisies de préfixes SI et conversions entre préfixes SI.
Pas moins de 11 préfixes sont gérés :- f : femto (10-15)
- p : pico (10-12)
- n : nano (10-9)
- μ : micro (10-6)
- m : milli (10-3)
- k : kilo (103)
- M : Méga (106)
- G : Giga (109)
- T : Téra (1012)
- P : Péra (1015)
- E : Exa (1018)
SETTINGS
, il te devient même possible d'obtenir une conversion automatique de ta saisie avec ou sans préfixes SI, vers le préfixe SI le plus pertinent pour présenter le résultat. - Symbole : donne accès à quelques fonctions et opérateurs non alphabétiques les plus usuels (les autres restant accessible via l'entrée Tout comme vu plus haut)
10) Menu VariableGo to top
Autre menu tranversal, celui appelé par la touche
Les noms de variables qu'il permet de saisir te son accessibles par types :
Seule exception, l'application Python qui dispose d'un menu variable spécifique.
VARIABLE. Il te liste ici l'ensemble des variables définies par l'utilisateur, accompagnées de leurs valeurs ! 👍
Les noms de variables qu'il permet de saisir te son accessibles par types :
- Alpha pour les 28 variables alphabétiques (26 lettres A à Z, auxquelles on ajoute r et θ)
- Fonction
- Vecteur
- Matrice
- Liste
Seule exception, l'application Python qui dispose d'un menu variable spécifique.
11) Application StatsGo to top
- Editeur Listes (affiché par défaut)
- Configuration
- et en fonction des données saisies ou du type de tâche sélectionnée :
- Graphe
- Résultat
- Graphe régress
26 listes sont gérées, nommées de List 1 à List 26, permettant aussi bien la saisie d'une série de données statistiques sur laquelle on va travailler dans cette application, que les calculs sur des listes dans l'application Calculs. S'ajoute dans ce dernier cas la liste List Ans pour le dernier résultat ayant pris la forme de liste.
Chaque liste peut contenir jusqu'à 999 éléments.
Chacune de ces listes peut de plus être nommée sur 8 caractères via la ligne ST, et ensuite appelée directement par ce nom (
List "NOM") dans les saisies de calculs si tu préfères.Ici il y a 2 cas possibles, en fonction de ta saisie précédente :
- soit la calculatrice te demande dabord la tâche que tu souhaites accomplir sur la série statistique que tu as saisie :
- Calcul statistiques
- Graphique
- Test d'hypothèse
- Intervalle de confiance
- soit la forme de ta saisie ne laisse aucune ambiguïté, et tu obtiens directement l'onglet de Configuration associé à la tâche devinée ; une sorte d'Intelligence Artificielle 😉
Tu peux par exemple obtenir les paramètres d'une série statistique à 1 ou 2 variables (onglet Résultats), et précisons que les quartiles respectent par défaut la définition non internationale utilisée au lycée Français.
Nombre de paramètres sont gérés pour chaque variable, et retournés dans l'onglet Résultats :
- paramètres de position :
- moyenne
- minimum et maximum
- 1er et 3e quartile (respectant par défaut la définition non internationale utilisée au lycée Français)
- médiane
- mode
- paramètres de dispersion :
- écart-type (population ou échantillon)
- effectifs et fréquences :
- effectif total
- effectif ou fréquence du mode
- paramètres sommatifs :
- somme des valeurs
- somme des carrés
- somme des produits (si 2 variables)
Nombre de modèles de régressions sont ici gérés, et tu obtiendras ici encore dans l'onglet Résultats les paramètres optimaux de l'équation :
- linéaire $mathjax$y=ax+b$mathjax$ou$mathjax$y=a+bx$mathjax$
- droite Med-Med $mathjax$y=ax+b$mathjax$
- quadratique $mathjax$y=ax^2+bx+c$mathjax$
- cubique $mathjax$y=ax^3+bx^2+cx+d$mathjax$
- quartique $mathjax$y=ax^4+bx^3+cx^2+dx+e$mathjax$
- logarithmique $mathjax$y=a+b\dot ln(x)$mathjax$
- exponentielle $mathjax$y=a\dot e^{bx}$mathjax$
- exposant $mathjax$y=a\dot b^x$mathjax$
- puissance $mathjax$y=a\dot x^b$mathjax$
- sinusoïdale $mathjax$y=a\dot sin(bx+c)+d$mathjax$
- logistique $mathjax$y=\frac{c}{1+a\dot e^{-bx}}$mathjax$
Divers types de diagrammes sont configurables, et leur tracé sera obtenu et visualisable sur l'onglet Graphe :
- nuage de points
- diagramme en boîtes (ou à moustaches), avec même la détection de valeurs aberrantes
- histogramme
- ligne brisée
- diagramme circulaire
- diagramme en barres
- probabilité normale
- densité normale
- Résulats
- Graphe régress
...!
- Tests Z à 1-2 échantillons ou 1-2 proportions
- Tests t à 1-2 échantillons ou de régression linéaire
- Tests χ² d'adéquation ou à 2 voies
- Test F à 2 échantillons
- Analyse de variance
- Résultats pour les résultats du test
- Graphe pour une interprétation graphique
- Intervalle Z à 1-2 échantillons ou 1-2 proportions
- Intervalle t à 1-2 échantillons
12) Application ProbabilitésGo to top
Petit passage par l'application Probabilités, dédiée aux questions de lois de probabilités. L'application présente ici 3 onglets te distinguant très clairement les différentes étapes à suivre dans la résolution de tes problèmes :
- Sélectionner (affichée par défaut)
- Configuration
- Résultats
Tu disposes de pas moins de 8 lois de probabilités au choix :
- 4 lois discrètes : binomiale, Poisson, géométrique, hypergéométrique
- 4 lois continues : Normale, χ², Student, Fisher
Enfin, nous arrivons sur la page Résultats et c'est un véritable régal.
Déjà, pour limiter tout risque d'erreur, Casio a pris le soin d'inclure sur cette page une ligne de rappel des paramètres de la loi saisis sur la page Configuration.
Au-delà de cela, l'interface utilisateur de la page Résultats y est en effet d'une intuitivité absolument remarquable, parlant littéralement le langage scolaire de l'utilisateur.
Tout se passe en effet autour d'une relation de probabilités. Il y a juste à saisir sélectionner un des paramètres de la relation et y saisir la valeur connue de l'énoncé, afin que la calculatrice résolve automatiquement le ou les autres paramètres et mette à jour la relation avec leur(s) valeur(s) ! 👍
La forme de la relation de probabilités autour de laquelle on travaille est de plus au choix, ce qui permet de couvrir un très large éventail de questions types :
Pour une meilleure compréhension, nous avons même une interprétation graphique directement intégrée à la page Résultats et mise à jour immédiatement à chaque modification !
Déjà, pour limiter tout risque d'erreur, Casio a pris le soin d'inclure sur cette page une ligne de rappel des paramètres de la loi saisis sur la page Configuration.
Au-delà de cela, l'interface utilisateur de la page Résultats y est en effet d'une intuitivité absolument remarquable, parlant littéralement le langage scolaire de l'utilisateur.
Tout se passe en effet autour d'une relation de probabilités. Il y a juste à saisir sélectionner un des paramètres de la relation et y saisir la valeur connue de l'énoncé, afin que la calculatrice résolve automatiquement le ou les autres paramètres et mette à jour la relation avec leur(s) valeur(s) ! 👍
La forme de la relation de probabilités autour de laquelle on travaille est de plus au choix, ce qui permet de couvrir un très large éventail de questions types :
- P(X=…)=… (lois discrètes uniquement - la saisie n'est autorisée que pour le premier paramètre)
- P(X≤…)=…
- P(X≥…)=…
- P(…≤X≤…)=… (le saisie du dernier paramètre n'est autorisée que pour une loi Normale)
Pour une meilleure compréhension, nous avons même une interprétation graphique directement intégrée à la page Résultats et mise à jour immédiatement à chaque modification !
13) Application Graphe&Table et zone graphiqueGo to top
L'application Graphe&Table présente 3 onglets :
- Fonction (affiché par défaut)
- Graphe
- Table
Pour chacune, l'application gère nombre de types de relations :
- fonctions cartésiennes y=f(x)
- fonctions polaires r=f(θ)
- fonctions paramétriques
- fonctions x=f(y) (dont fonctions réciproques)
- inéquations (y≤f(x), x>f(y), ...)
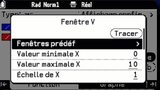
Rien de méchant, la configuration en question est préremplie (et si besoin plusieurs configurations prédéfinies sont accessibles). Cette popup de configuration est donc simplement montrée à l'utilisateur lorsqu'il tente d'accéder à la représentation graphique ; il peut très bien ne rien y changer et l'appliquer immédiatement grâce au bouton d'action Tracer justement présenté en toute première ligne. Mais c'est ici encore une nouveauté d'une pertinence remarquable, rien que de voir cette configuration pendant un court instant donnant ainsi davantage de sens dans l'esprit de l'utilisateur à la représentation graphique qui va suivre ! 👍
Dans ce cas ces variables sont automatiquement détectées avec possibilité pour chacune de configurer les bornes et pas des valeurs qu'elle doit prendre, et d'obtenir ainsi une animation permettant d'observer son effet sur l'aspect de la courbe.
C'est-à-dire que Graph&Table fusionnerait en fait les fonctionnalités de non pas 2 mais 3 applications intégrées à la Graph 90+E : Graphe, Table et G-dynamique.
Nous ignorons donc si l'annonce par Casio de fonctionnalités équivalentes à G-dynamique pour la seule rentrée 2025 était une erreur, ou bien si des améliorations sont prévues dans ce cadre.
Sur Graph Math+, par défaut nous comptons un peu moins, 379×165 pixels, à cause des onglets affichés en permanence en bas d'écran.
Toutefois, nous découvrons qu'il est possible de masquer ces onglets avec la touche flèchée page suivante, et dans ce cas nous obtenons bien les mêmes 379×187 pixels.
Autre belle évolution, lorsque la fenêtre graphique est mal configurée, ou en cas de définition de fonctions assez exotiques, il arrivait que rien ne soit visible à l'écran car tout ce qui était censé être tracé était hors fenêtre. Et dans ce cas les élèves étaient bien souvent perdus. Dans ce cas la Graph Math+ prévient désormais l'utilisateur avec un message d'avertissement "graphique Hors plage de tracé".
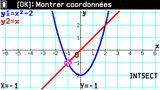 Nous apprécions au passage une interface très loquace, nous faisant quasiment des phrases en alignant de longues lignes de mots, et remarquons entre autres l'utilisation déjà évoquée de messages d'aide en ligne fort bienvenus dans la barre d'état en haut d'écran.
Nous apprécions au passage une interface très loquace, nous faisant quasiment des phrases en alignant de longues lignes de mots, et remarquons entre autres l'utilisation déjà évoquée de messages d'aide en ligne fort bienvenus dans la barre d'état en haut d'écran.On retrouve bien évidemment tous les outils pertinents pour travailler sur les représentations graphiques : suivi de courbe, images et antécédents (avec même les traits de constructions), zéros, ordonnée à l'origine, points d'intersections, tangente en un point, nombre dérivé, intégrale, aire entre deux courbes, etc.
Superbe innovation ici aussi, le menu contextuel de la touche
...te permet d'accompagner le tableur de valeurs d'une représentation graphique en nuage de points, et même d'y mettre en évidence la valeur sélectionnée ! 👍
14) Application Python, zone graphique écran et getkey()Go to top
L'application présente 2 onglets :
- Editeur (affiché par défaut)
- Shell
Jusqu'à présent, les applications Python des calculatrices faisaient quasiment toutes démarrer l'utilisateur dans la liste des scripts, parfois même pire dans un explorateur de fichiers (exception avec la HP Prime qui s'ouvrait directement dans la console Python). Ce cas mis à part, l'utilisateur devait donc de façon quasi systématique faire la manipulation permettant de créer un script ou pire fichier après avoir navigué vers le bon dossier, et d'en saisir le nom au clavier alphabétique. C'était entre autres le cas pour la Graph 90+E.
Qu'est-ce que c'était lourd, long et compliqué... Rajoutons de plus que nous sommes hélas de plus en plus sur des générations d'utilisateurs qui ont de plus en plus de mal à comprendre et distinguer fichiers et dossiers, les appareils numériques qu'ils utilisent ayant tendance à leur masquer cet aspect informatique, et ne parlons même pas de dossier racine ou encore dossiers compressés (archives).
Qu'est-ce que c'était lourd, long et compliqué... Rajoutons de plus que nous sommes hélas de plus en plus sur des générations d'utilisateurs qui ont de plus en plus de mal à comprendre et distinguer fichiers et dossiers, les appareils numériques qu'ils utilisent ayant tendance à leur masquer cet aspect informatique, et ne parlons même pas de dossier racine ou encore dossiers compressés (archives).
En effet justement, quand on fait du Python en classe, le but est le plus souvent de saisir et tester un petit script (et non de réutiliser un script déjà existant), dans la plupart des cas sans volonté de le conserver. On réutilise et conserve plutôt nos scripts dans le cadre de projets, un cas d'utilisation moins fréquent à la fois en fréquence dans le temps et ainsi qu'en effectif car concernant moins d'utilisateurs.
Rassure-toi, l'utilisateur conserve bien évidemment la possibilité de sauvegarder son script après saisie si il le souhaite, grâce au menu contextuel de la touche
...avec la possibilité donc pour les utilisateurs un peu plus experts de choisir un nom de fichier autre que module.py, évitant ainsi l'écrasement du script lors de la prochaine saisie.
Comme sur Graph 90+E, nous continuons à bénéficier de l'indentation automatique ainsi que de la coloration syntaxique.
Nous notons au passage que l'éditeur de script est capable d'afficher jusqu'à 9 lignes de code par écran, contre les 7 trop grosses lignes de la Graph 90+E (qui venaient du fait que l'interface Graph 90+E était en fait une version agrandie d'un facteur 3 de l'interface Graph 35+E II), qui outre l'aspect visuel avaient également le défaut de brider lourdement le caractère global de la visualisation des scripts saisis.
CATALOGqui présente les instructions et fonctions Python relatives aux différentes bibliothèques.
Et comme déjà évoqué, on peut faire appel à la table des caractères spéciaux pour tout ce qui n'est pas directement disponible au clavier, et elle a l'énorme avantage de s'affiche en bas d'écran à la place des onglets, laissant donc l'intégralité du script saisi visible pendant son utilisation ! 👍
Déjà, nous remarquons que l'intérpréteur est toujours le même que sur Graph 90+E, Micropython toujours dans la même version 1.9.4.
Le script saisi dans l'onglet Editeur est lancé automatiquement par la commande
from module import *.Prenons par exemple un petit script, pour calculer la moyenne arithmétique de 3 notes. Nous avons l'immense plaisir de constater dans l'onglet Shell que Casio a tenu compte d'un de nos retours. En effet la touche
VARIABLEsi tapée depuis cette vue liste les variables et fonctions définies et permet ainsi leur saisie rapide, génial ! 👍
Explorons un petit peu les bibliothèques disponibles. Nous notons plusieurs bibliothèque standard :
- math pour les fonctions mathématiques
- random pour l'aléatoire
- et 2 bibliothèques de tracé :
- turtle pour les tracés à la tortue
- matplotlib.pyplot pour les tracés dans un repère
Elle fournit d'une part des fonctions de tracé par pixels, qui sont justement utilisées par les bibliothèques de tracé précédentes : set_pixel(), get_pixel(), draw_string(), clear_screen().
Précisons que pour de meilleures performances et tracés plus propres, ces fonctions bénéficient d'un double buffering. Les tracés demandés ne seront pas immédiatement visibles car réalisés hors écran, et uniquement affichés d'un seul coup lors du prochain appel show_screen().
- Code: Tout sélectionner
from casioplot import *
for i in range(192):
set_pixel(i * 2, i)
show_screen
Dernière nouvelle excellente, la bibliothèque casioplot a ici enfin été étendue avec une nouvelle fonction getkey() permettant d'identifier les touches tapées par l'utilisateur. Qui plus est Casio a été au top, le test en question étant non bloquant. Le développement de projets Python sur Graph Math+ va donc pouvoir atteindre un tout nouveau niveau, avec notamment la programmation d'interfaces ou jeux directement contrôlables au clavier par l'utilisateur ! 🎉
- Code: Tout sélectionner
from casioplot import *
while True:
key = getkey()
clear_screen()
draw_string(0, 0, str(key))
show_screen()
Et bien en fait c'est extrêmement simple contrairement à d'autres modèles. Le code identifiant chaque touche pressée est un nombre à 2 chiffres, avec :
- au chiffre des dizaines le numéro de la rangée en partant du haut
- au chiffre des unités le numéro de la colonne en partant de la gauche
ONet
ACne peut être détectée par cette fonction, car interrompant justement le script en cours d'exécutation.
15) Application EquationsGo to top
Dans l'application Equations, un premier onglet Type affiché par défaut te permet de choisir le type d'équations que tu souhaites résoudre  ntss
ntss
 ntss
ntss- Système
- Polynomiale
- Solveur
Le choix Système te permet de résoudre des systèmes d'équations linéaires.
Les onglets à parcourir dans l'ordre sont ici :
Les onglets à parcourir dans l'ordre sont ici :
- Inconnus pour choisir le nombre d'inconnus et donc d'équations, jusqu'à 6 au maximum
- Editeur pour saisir les coefficients des équations ainsi configurées
- Résultats pour obtenir la ou les solutions, avec gestion des cas avec infinité de solutions ou aucune solution, ainsi qu'une gestion des solutions exactes QPiRac
Le choix Polynomiale te permet de trouver les racines de polynômes.
Les onglets épinglés t'indiquant les étapes à suivre sont alors ici :
Les onglets épinglés t'indiquant les étapes à suivre sont alors ici :
- Degrés pour choisir le degré du polynôme, jusqu'à 6
- Editeur pour saisir les coefficients du polynôme ainsi configuré
- Résultats pour obtenir les racines, au format exact QPiRac si pertinent
Enfin, le choix Equation te permet de résoudre une équation saisie librement sous la forme de ton choix. L'équation peut même faire appel à plusieurs variables dont tu pourras alors préciser les valeurs avant de la résoudre pour l'inconnue choisie.
16) Application SuitesGo to top
L'application Suite te permet de travailler avec des suites numériques.
Elle dispose de 2 onglets :
Elle dispose de 2 onglets :
- Suite (affiché par défaut)
- Table
Sur Graph 90+E les définitions de suites étaient pénibles.
En effet, rang initial et dans le cas de suites récurrentes terme initial, étaient à définir et consulter sur un écran distinct de celui de saisie de la définition par le terme général ou bien de la relation de récurrence.
C'était générateur de nombre d'erreurs chez les élèves....
En effet, rang initial et dans le cas de suites récurrentes terme initial, étaient à définir et consulter sur un écran distinct de celui de saisie de la définition par le terme général ou bien de la relation de récurrence.
C'était générateur de nombre d'erreurs chez les élèves....
Pour chacune plusieurs formes de définitions te sont proposées au choix :
- terme général
- récurrence d'ordre 1
- récurrence d'ordre 2
La représentation graphique associée est également accessible sur ce même onglet via la touche menu contextuel
..., soit à la place du tableau soit en plus.
Dans le cas de suites définies par récurrences, il est possible d'opter à la place du nuage de points pour une représentaiton dite en toile d'araignée et même d'animer son tracé étape par étape :
17) Application ParamètresGo to top
Les différents paramétrages possibles sont dabord présentés sous la forme d'un menu plein écran, puis une fois ton choix effectué sous la forme d'onglets de bas d'écran te permettant de passer au suivant ou précédente.
Un des premiers réglages concerne la langue de l'interface de la calculatrice, avec 5 choix possibles :
- English pour l'Anglais
- Español pour l'Espagnol
- Français
- Italiano pour l'Italien
- Português pour le Portugais
- le Chinois qui sera peut-être développé et rajouté ultérieurement
- et de façon moins surprenante l'Allemand, l'Allemagne ayant fait en effet le choix surprenant d'interdire les calculatrices graphiques d'entrée et milieu de gamme à l'horizon de la session 2030 de l'Abitur, alors que paradoxalement les simples calculatrices scientifiques et calculatrices graphiques formelles haut de gamme restent autorisées
Tu peux également configurer entre autres :
- le type de piles AAA utilisées (alcalines, ou rechargeables Ni-MH), très important à régler correctement pour la bonne détection de l'état des piles
- la luminosité du rétroéclairage
- les paramètres d'économie d'énergie : délais d'inactivité avant arrêt du rétroéclairage de l'écran puis extinction de la calculatrice
En France avec les énormes volumes de calculatrices graphiques en circulation chaque année, un gros problème est la perte ou le vol. Cela peut concerner aussi bien les élèves avec leur machine individuelle, que les enseignants disposant d'un stock de machines prêtées aux élèves.
Pour identifier ta calculatrice graphique Casio, tu pouvais conserver une photo du numéro de série à code barre présent sur un autocollant dans le compartiment des piles.
Sauf que cet autocollant pouvait être perdu, abîmé, ou volontairement retiré par un voleur.
La Graph 90+E te permettait quelque chose d'un peu plus poussé qui aurait pu être génial, la signature électronique de ta calculatrice. Tu pouvais en effet y enregistrer en mémoire Flash des noms d'utilisateur et organisation, informations montrées à chaque extinction de la calculatrice, et protéger leur modification par un mot de passe.
A priori une belle protection contre la perte ou le vol... Sauf que Casio a également pensé aux utilisateurs oubliant leur mot de passe, ou acheteurs de calculatrices d'occasion à qui on ne communiquerait pas le mot de passe. Une combinaison de démarrage unique te permet d'effacer ce mot de passe et les données associées sur l'ensemble des Graph 90+E. Trouvable sur Internet, elle permet à n'importe quel voleur suffisamment bien informé de remaquiller immédiatement la calculatrice en effaçant ou écrasant ta signature par autre chose.
Pour identifier ta calculatrice graphique Casio, tu pouvais conserver une photo du numéro de série à code barre présent sur un autocollant dans le compartiment des piles.
Sauf que cet autocollant pouvait être perdu, abîmé, ou volontairement retiré par un voleur.
La Graph 90+E te permettait quelque chose d'un peu plus poussé qui aurait pu être génial, la signature électronique de ta calculatrice. Tu pouvais en effet y enregistrer en mémoire Flash des noms d'utilisateur et organisation, informations montrées à chaque extinction de la calculatrice, et protéger leur modification par un mot de passe.
A priori une belle protection contre la perte ou le vol... Sauf que Casio a également pensé aux utilisateurs oubliant leur mot de passe, ou acheteurs de calculatrices d'occasion à qui on ne communiquerait pas le mot de passe. Une combinaison de démarrage unique te permet d'effacer ce mot de passe et les données associées sur l'ensemble des Graph 90+E. Trouvable sur Internet, elle permet à n'importe quel voleur suffisamment bien informé de remaquiller immédiatement la calculatrice en effaçant ou écrasant ta signature par autre chose.
Une idée aurait été de conserver le mot de passe et supprimer la possibilité offerte à n'importe qui de le réinitialiser, mais ce n'est apparemment pas ce qui a été retenu.
Tout à l'inverse, Casio a simplement supprimé le mot de passe ; c'est-à-dire que n'importe qui peut désormais changer la signature de la calculatrice. En remplacement, Casio affiche désormais un numéro de série logiciel inaltérable dont il te suffira de conserver une photo.
18) Application Mode examen et définition complète écranGo to top
Le mode examen qu'est-ce que c'est ? C'est un mode de fonctionnement spécial de ta calculatrice, dont l'activation est exigée en France depuis la session d'examens 2020, et régi par la circulaire n°2015-178 du 1er octobre 2015. L'une des caractéristiques de ce mode est d'interdire la consultation de toute donnée qui auraient été préchargée en mémoire avant l'activation du mode examen. Il est donc destiné à être activé au tout début d'une épreuve.
Sur la Graph 90+E, l'invocation du mode examen nécessitait d'allumer la calculatrice en maintenant les touches
7et
COSenfoncées. Moyen mnémotechnique, en fonctions alphabétiques ces touches correspondaient respectivement à M et E, ce qui donnait Mode Examen. Mais cela n'en restait que peu accessible pour qui ne connaissait pas cette astuce ou ne réalisait pas cette manipulation assez souvent, et ne lisait pas l'aide en ligne du mode examen disponible dans la calculatrice.
Il t'y est par exemple rappelé que le mode d'examen consomme davantage d'énergie et qu'il te faudra donc le désactiver le plus tôt possible en fin d'épreuve. En effet la calculatrice ne s'éteint jamais complètement en mode examen, c'est juste l'écran qui est éteint, le processeur restant éveillé pour faire clignoter la diode examen rouge présente sur la tranche supérieure de la calculatrice.
Pour les petits malins qui activent leur mode examen avant leur épreuve afin de pouvoir arriver à cette dernière avec une mémoire non vide, Casio a prévu la parade. Plus aucun besoin pour les surveillants de s'embêter à trouver une calculatrice compatible ou configurer en urgence un ordinateur pour désactiver le mode examen, l'application propose dans ce cas la possibilité directe de réactiver le mode examen, c'est-à-dire de vider à nouveau toute éventuelle donnée mémoire !
Ajoutons à cela une aide en ligne exhaustive.
- déjà, à l'écran d'accueil de l'application Mode Examen, ce dernier précisant de plus :
- la configuration du mode examen (France dans notre cas) et donc sa conformité avec la réglementation
- la version système, au cas où des failles aient été identifiées et nécessitent une mise à jour
- un drapeau R bleu clignotant en haut à droite de l'écran (de façon rapide puis ralentie après 15 minutes, une façon de vérifier si le mode examen a bien été activé en début d'épreuve et pas avant)
- une diode rouge clignotante sur la tranche supérieure de la calculatrice, le clignotant se poursuivant même calculatrice éteinte
- une bordure de couleur autour de l'écran, vert dans le cas de la configuration pour la France
Précisons plusieurs restrictions du mode examen dans son implémentation par Casio :
- le rétroéclairage de l'écran peut être diminué mais jamais éteint complètement, ce qui permet un meilleure visibilité pour les surveillants
- toutes les données saisies, y compris celles qui habituellement vont en mémoire de stockage Flash comme les fichiers de scripts Python, sont stockés obligatoirement en mémoire principale RAM, ce qui te limite donc à 64K de données
- toutes les données saisies sont perdues en cas de :
- redémarrage de le calculatrice (bouton RESTART au dos ou plantage)
- rupture de l'alimentation (piles à plat, retrait d'une pile, changement de piles)
19) Application Base-NGo to top
La Graph 90+E permettait de faire appel à différentes bases numériques pour tes calculs, mais c'était une fonctionnalité relativement cachée et fort mal intégrée.
Depuis l'application de calcul historique il fallait modifier le paramètre Mode sur une autre valeur que Comp. Le comportement de l'application de calcul changeait alors radicalement, désactivant la saisie naturelle, l'accès à nombre de fonctions scientifiques au clavier, ou encore la possibilité de remonter dans l'historique des calculs.
Un fonctionnement extrêmement déconcertant pour l'utilisateur.
Depuis l'application de calcul historique il fallait modifier le paramètre Mode sur une autre valeur que Comp. Le comportement de l'application de calcul changeait alors radicalement, désactivant la saisie naturelle, l'accès à nombre de fonctions scientifiques au clavier, ou encore la possibilité de remonter dans l'historique des calculs.
Un fonctionnement extrêmement déconcertant pour l'utilisateur.
La toute nouvelle application Base-N nous apporte en effet une toute nouvelle interface dédiée à ce type de calculs !
De haut en bas on distingue :
- la ligne de saisie pour tes nombres ou calculs
- la base numérique à utiliser pour les nombres de ta saisie dont tu ne précises pas la base, modifiable avec la touche
FORMAT
- et enfin le résultat indiqué simultanément dans pas moins de 4 bases différentes : hexadécimale, décimale, octale et binaire
Nombre d'opérations binaires sont alors possibles :
- and : et
- or : ou
- xor : ou exclusif
- xnor : non ou exclusif
- Neg : négatif/opposé (complément à 2)
- Not : non/négation (complément à 1)
20) Application Mémoire : Capacités, formats de fichiers supportés et point sur les applications additionnellesGo to top
L'application Mémoire présente 2 onglets :
- Mémoire princi (affiché par défaut)
- Mémoire stock
Sur Graph 90+E, cet espace de stockage en mémoire RAM indiquait après vidage une capacité de 61,904 Ko, pour une capacité RAM totale de 8 Mio.
Notre première capture de la mémoire principale Graph Math+ ci-contre indique 59,484 Ko libres, sans vidage préalable. Cela suggère donc qu'il n'y aurait pas de changement sur la capacité de la mémoire principale (toujours offert par un bloc de 64 Kio), même si la capacité RAM pourrait être différente.
Sur la Graph 90+E, cet espace de stockage en mémoire Flash indiquait après vidage une capacité de 16,248 Mo, pour une capacité Flash totale de 32 Mio (l'autre moitié de la puce étant réservée au stockage du système d'exploitation). En sortie d'usine, l'espace de stockage libre comptait dans les 6 Mo.
Notre première capture de la mémoire de stockage ci-contre indique 4,427776 Mo libres, sans vidage préalable donc. Cela suggère qu'il n'y a pas de changement sur la capacité de la mémoire de stockage (toujours offerte par une partition de 16 Mio), et probablement pas non plus sur la capacité totale de la puce Flash.
Si les caractéristiques matérielles ne semblent pas bouger jusqu'ici, il n'en va pas de même du logiciel. En effet cette dernière capture nous suggère une évolution logicielle majeure avec un nouveau format de fichier pour les variables : .g4m, en lieu et place du .g3m de la Graph 90+E qui ne serait plus supporté selon le manuel. Pour qu'un nouveau format ait été nécessaire, c'est qu'il y a des changements significatifs internes au système.
Pour les images le manuel indique également un nouveau format .g4p, à la différence qu'ici l'ancien format .g3p de la Graph 90+E serait encore supporté.
Le reste des types de fichiers supportés l'étaient déjà sur Graph 90+E : .py pour les scripts Python, .bmp pour les images, et .csv pour l'importation de données en tant que feuille de calculs, matrices ou série statistique.
C'est-à-dire que plusieurs autres types de fichiers compatibles avec la Graph 90+E ne seraient plus supportés sur Graph Math+ :
- Nous pouvons citer les fichiers de textes et documents .txt, .g1e, .g2e et .g3e, ce qui n'est pas une surprise puisque la Graph Math+ n'intègre pas à ce jour l'application d'édition de documents scientifiques eActivity.
- La Graph 90+E permettait l'installation hors mode examen d'applications additionnelles, officielles ou non, par ajout de fichiers .g3a. Ces applications écrites en langage C ou assembleur permettaient d'aller beaucoup plus loin dans le processus créatif qu'avec les programmes en langage Casio Basic ou Python. Nous notons que ces fichiers .g3a ne sont plus supporés et que la Graph Math+ ne permet donc plus l'installation d'applications additionnelles, du moins actuellement dans la version 1.00 du système d'exploitation. Nous ignorons à ce jour si c'est temporaire, le temps de développer de façon similaire un nouveau format de fichier .g4a, ou bien définitif.
- De façon similaire, le format .g3l qui permettait l'installation de langues supplémentaires (utilisés uniquement pour le Russe) n'est plus supporté.
- Citons également .g3b pour les images animées, spécifiques à l'application additionnelle Plot Image elle aussi absente.
21) Echantillons et émulateursGo to top
Envie toi aussi de pouvoir tester et donc aller plus loin dans l'exploration de cette petite merveille que sera la Graph Math+ à la rentrée 2024 ?

 10 avril 2024, un émulateur Graph Math+ sera téléchargeable gratuitement pour ajout à ta clé USB d'émulation Casio (émulateur utilisable directement sans installation sous Windows). Attention l'émulateur ne fonctionnera que si la clé USB d'émulation Casio officielle est branchée sur ton ordinateur. Enseignant, si tu ne disposes pas encore de cette clé USB n'attends pas d'en avoir besoin, demande la gratuitement dès maintenant.
10 avril 2024, un émulateur Graph Math+ sera téléchargeable gratuitement pour ajout à ta clé USB d'émulation Casio (émulateur utilisable directement sans installation sous Windows). Attention l'émulateur ne fonctionnera que si la clé USB d'émulation Casio officielle est branchée sur ton ordinateur. Enseignant, si tu ne disposes pas encore de cette clé USB n'attends pas d'en avoir besoin, demande la gratuitement dès maintenant.
Courant avril 2024, les premiers exemplaires de test seront expédiés aux enseignants en ayant fait la demande. Il suffit pour cela d'être prof de Mathématiques ou sciences en exercice dans un lycée de France (aussi bien en métropole qu'en outre-mer). Si ce n'est pas déjà fait alors demander le vite, c'est gratuit, et il n'y en aura pas pour tout le monde...
Rentrée 2024, un émulateur en ligne Graph Math+ tournant directement dans ton navigateur Internet sera rajouté à la plateforme ClassPad.net. Cet émulateur te sera accessible gratuitement depuis ton compte enseignant ClassPad.academy. Tu ne disposes pas encore d'un compte ClassPad.Academy ? Va vite le créer, c'est gratuit pour les enseignants !
Courant avril 2024, les premiers exemplaires de test seront expédiés aux enseignants en ayant fait la demande. Il suffit pour cela d'être prof de Mathématiques ou sciences en exercice dans un lycée de France (aussi bien en métropole qu'en outre-mer). Si ce n'est pas déjà fait alors demander le vite, c'est gratuit, et il n'y en aura pas pour tout le monde...
Rentrée 2024, un émulateur en ligne Graph Math+ tournant directement dans ton navigateur Internet sera rajouté à la plateforme ClassPad.net. Cet émulateur te sera accessible gratuitement depuis ton compte enseignant ClassPad.academy. Tu ne disposes pas encore d'un compte ClassPad.Academy ? Va vite le créer, c'est gratuit pour les enseignants !
ConclusionGo to top
La Graph Math+ est apparemment le fruit d'une très riche et mûre réflexion de la part de Casio, la synthèse d'années de retours de la part d'enseignants et utilisateurs concernant la Graph 90+E.
Le travail effectué par Casio autour de la nouvelle interface de la Graph Math+ depuis deux ans est clairement de très haute facture.
On peut citer les différentes vues offertes dans les diverses applications par les onglets de bas d'écran, permettant selon l'application :
Il y a clairement eu une réflexion très profonde autour de l'intuitivité, la simplicité, l'aide à la compréhension et donc entre autres la pédagogie.
Si Casio a tout changé dans l'interface, chaque nouveauté a visiblement une excellente raison d'être à l'endroit et sous la forme où nous la trouvons, tout a été pesé et pensé, rien n'a été laissé au hasard !
Nous ne pouvons donc que nous incliner devant les compétences hautement remarquables dont ont su faire preuve les enseignants partenaires qui ont aidé Casio à imaginer et concevoir ce nouveau produit en réponse aux différents retours et problématiques :
Le travail effectué par Casio autour de la nouvelle interface de la Graph Math+ depuis deux ans est clairement de très haute facture.
On peut citer les différentes vues offertes dans les diverses applications par les onglets de bas d'écran, permettant selon l'application :
- la consultation de différentes représentations des données, permettant d'avancer la résolution d'un problème de façon transversale sous diverses représentations
- ou bien une énumération claire des étapes successives à suivre
- les nouvelles applications et interfaces intuitives pour le mode examen et les bases numériques
- l'application Python immédiatement prête à l'emploi
- tous les éléments de définition d'une suite présents sur un même écran
Il y a clairement eu une réflexion très profonde autour de l'intuitivité, la simplicité, l'aide à la compréhension et donc entre autres la pédagogie.
Si Casio a tout changé dans l'interface, chaque nouveauté a visiblement une excellente raison d'être à l'endroit et sous la forme où nous la trouvons, tout a été pesé et pensé, rien n'a été laissé au hasard !
Nous ne pouvons donc que nous incliner devant les compétences hautement remarquables dont ont su faire preuve les enseignants partenaires qui ont aidé Casio à imaginer et concevoir ce nouveau produit en réponse aux différents retours et problématiques :
- Djelloul Hidra, professeur agrégé de Mathématiques (académie de Nantes), et justement également consultant formateur pour CASIO France depuis bientôt 12 ans
- Thomas Lechenne, professeur agrégé de Mathématiques (académie de Besançon), et également consultant pour CASIO France depuis 16 ans
- Yves Coudert, professeur agrégé de Mathématiques s'occupant également de la spécialité NSI au Lycée Le Bon Sauveur à Le Vésinet (académie de Versailles), et également consultant pour CASIO France depuis 15 ans et demi