2018 annale
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: modl
Type : Classeur 3.6
Page(s) : 14
Taille Size: 1.06 Mo MB
Mis en ligne Uploaded: 13/06/2021 - 19:42:54
Uploadeur Uploader: modl (Profil)
Téléchargements Downloads: 5
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2763238
Type : Classeur 3.6
Page(s) : 14
Taille Size: 1.06 Mo MB
Mis en ligne Uploaded: 13/06/2021 - 19:42:54
Uploadeur Uploader: modl (Profil)
Téléchargements Downloads: 5
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2763238
Description
PC Deuxième Année Année 2017-2018
Physique : Evaluation de Fin de Semestre
Mardi 12 juin 2018 Durée : 3h00
Barème indicatif :
Le sujet est constitué de deux parties indépendantes
Barème indicatif sur 40:
Partie 1 : exercice 1 sur 15 points ; exercice 2 sur 10 points.
Partie 2 sur 15 points.
Document autorisé : une feuille de synthèse recto manuscrite originale
Calculatrice tout type non connectée (collège ou lycée) autorisée
Téléphone portable non autorisé
PARTIE 1 : Etude d’un microscope holographique numérique
Exercice 1 : Enregistrement d’un hologramme
Une photographie numérique classique est formée à partir de l’enregistrement, sur une matrice de
capteurs CCD, du signal lumineux reçu par chacun de ces capteurs considérés comme des détecteurs
quadratiques. Dans le cas des appareils numériques classiques, l’information contenue dans la phase
des rayons lumineux n’est donc pas enregistrée. Un dispositif holographique numérique permet
l’enregistrement de cette information de phase, et donc de retranscrire l’intégralité de l’information
portée par l’onde lumineuse reçue (d’où le terme d’hologramme, du grec holos qui signifie « en
entier »). Le dispositif étudié ici permet l’enregistrement d’hologrammes numériques pour
l’observation d’objets de petite taille (cellules, molécules) circulant dans un liquide.
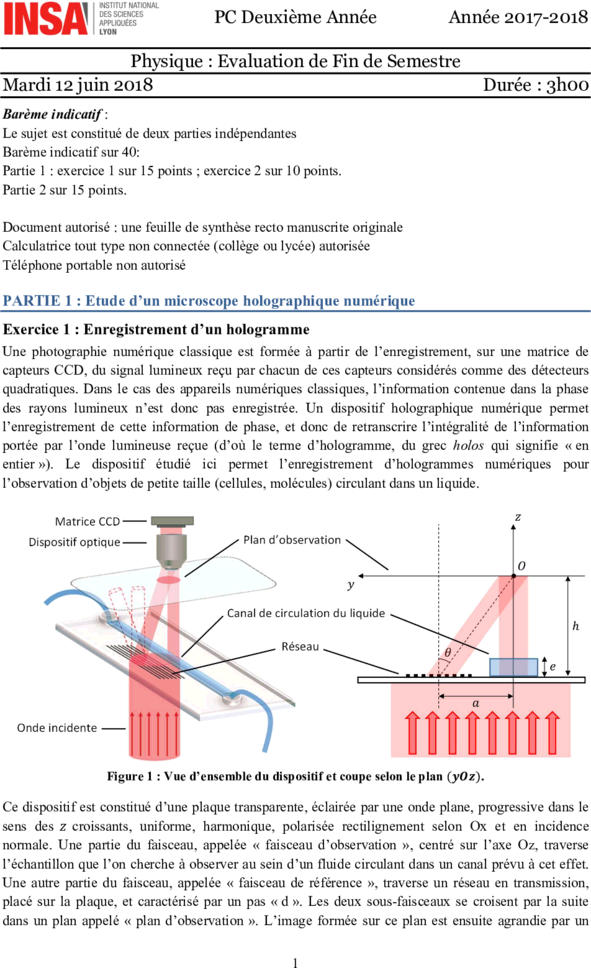
Figure 1 : Vue d’ensemble du dispositif et coupe selon le plan (????????????).
Ce dispositif est constitué d’une plaque transparente, éclairée par une onde plane, progressive dans le
sens des ???? croissants, uniforme, harmonique, polarisée rectilignement selon Ox et en incidence
normale. Une partie du faisceau, appelée « faisceau d’observation », centré sur l’axe Oz, traverse
l’échantillon que l’on cherche à observer au sein d’un fluide circulant dans un canal prévu à cet effet.
Une autre partie du faisceau, appelée « faisceau de référence », traverse un réseau en transmission,
placé sur la plaque, et caractérisé par un pas « d ». Les deux sous-faisceaux se croisent par la suite
dans un plan appelé « plan d’observation ». L’image formée sur ce plan est ensuite agrandie par un
1
dispositif optique puis enregistrée par la matrice de capteurs CCD (ces deux dispositifs ne sont pas
étudiés ici).
Le centre du réseau est situé à la distance ???? de l’axe Oz (axe du faisceau d’observation). Le plan
d’observation est positionné à une hauteur ℎ de la plaque support. Un liquide d’indice ???? circule dans le
canal d’épaisseur ????. Le reste du dispositif est placé dans l’air que l’on prendra d’indice égal à 1.
1) Expliquer pourquoi le réseau donne lieu à une déviation du faisceau de référence, qui peut
donc croiser le faisceau d’observation.
2) Quel est le type d’interféromètre réalisé ici ?
Le dispositif a pour dimensions ℎ = 1 m et ???? = 400 mm et est éclairé par un faisceau
monochromatique dont la longueur d’onde est ???? = 633 nm dans le vide. On souhaite que le faisceau
d’observation croise le faisceau d’ordre 1 issu du réseau au point O. On considérera, pour simplifier le
problème, que la distance ℎ est suffisamment grande pour faire l’hypothèse que ce faisceau d’ordre 1
est une onde plane (cf. Figure 2).
3) Calculer l’angle de déviation nécessaire ???? = ???? pour que les deux faisceaux se croisent au
point O (cf. Figure 1). En déduire le pas du réseau et exprimer le nombre de fentes par
millimètres correspondant.
4) Exprimer la différence de chemin optique ???? entre les deux rayons qui interfèrent au point ????
en fonction de ????, ℎ, ???? et ???? et déterminer ???? pour que ???? = 0 en prenant ???? = 1,5. Dans toute la
suite du problème on considérera que cette condition sur e est vérifiée.
On considère donc les deux faisceaux (observation et référence) comme étant deux ondes planes et
uniformes dont les directions de propagation forment un angle ???? ( figure 2) :
Faisceau de référence Faisceau d’observation
Figure 2 : Intersection des deux sous-faisceaux, qui sont considérés comme deux ondes planes, dans le plan
d'observation.
5) Exprimer la différence de chemin optique ???? entre les deux ondes plane en un point quelconque
situé dans le plan d’observation en sachant qu’au point ????, ???? = 0.
6) Que va-t-on observer dans le plan d’observation ?
7) Donner toutes les caractéristiques de la figure qui résulte de la superposition de ces deux
faisceaux (on supposera qu’ils ont, au point considéré, la même intensité lumineuse ???? ).
2
8) Etablir, à l’aide d’une démonstration rigoureuse, que l’intensité lumineuse reçue dans le plan
d’observation dans ces conditions s’écrit sous la forme ????(????) = ???? 1 + cos Φ(y) . Exprimer
???? en fonction de ???? et Φ(y) en fonction de la distance interfrange ???? et de ????.
On suppose que des cellules sont présentes au sein du liquide qui remplit le canal. Celles-ci ont un
indice optique et un coefficient d’atténuation lumineuse différents de ceux du liquide.
9) En quoi cela va-t-il modifier la figure d’interférences obtenue grâce au dispositif ?
Exercice 2 : Observation d’un hologramme
L’image obtenue dans le plan d’observation grâce à la matrice de capteurs CCD peut ensuite être
imprimée sur un support transparent, que l’on appelle hologramme. Cet objet a une transparence qui
varie en fonction de l’intensité de l’onde qu’il a reçue pendant l’impression de l’image en chaque point
de sa surface de coordonnées (????, ????). Cette variation de transparence est associée à une « fonction de
transmission » ????(????, ????) (comprise entre 0 et 1) qui permet de calculer l’amplitude des rayons lumineux
transmis lorsqu’ils traversent l’hologramme éclairé par une onde plane (cette fonction vaut 1 dans les
zones parfaitement transparentes et 0 dans les zones parfaitement opaques).
Si on imprime la figure d’interférence obtenue dans le cas de l’exercice 1 (en absence de cellules dans
le liquide), on obtient un hologramme qui possède une fonction de transmission sinusoïdale de la
forme:
1 2???????? ???? ????
????(????) = 1 + cos pour − <????<+
2 ???? 2 2
L’image de l’hologramme (de largeur L et de hauteur H) et le profil de la fonction de transmission qui
lui est associé sont montrés sur la figure 3. En dehors de l’hologramme (???? < −????/2 ou ???? > ????/2) la
fonction de transmission est nulle (opaque). De plus la hauteur ???? de la zone de l’hologramme éclairée
est grande vis-à-vis de la longueur d’onde (les échelles ne sont pas respectées sur la figure).
a) ????
????(????)
1
b) ????
???? 0 ????
− ????
+
2 2
Figure 3 : a) Hologramme obtenu en imprimant la figure d’interférences de l’exercice 1 sur un support
transparent ; b) Fonction de transmission sinusoïdale associée à l’hologramme.
3
On éclaire cet hologramme à l’aide du même laser que celui utilisé précédemment, en incidence
normale, et on étudie le phénomène de diffraction engendré. Chaque élément de surface ???? ⋅ ????????
(surface d’Huygens élémentaire) peut être considéré comme une source secondaire de l’onde plane
incidente dont l’amplitude de l’onde réémise est égale à : ????(????) × ???? × ???? × ???????? (???? étant une constante
associée à l’amplitude de l’onde incidente).
1) Exprimer la différence de marche entre un rayon issu d’une fente élémentaire en ???? et le rayon
de référence issu du centre de l’hologramme en ???? = 0 dans une direction d’observation ????.
(Vous pourrez faire un petit schéma pour appuyer votre démonstration).
2) Donner l’expression complexe de l’onde émise par cette surface élémentaire dans la direction
d’observation. Dans cette expression, vous exprimerez le cosinus en fonction d’exponentielles
complexes (en utilisant la formule d’Euler), et le nombre d’onde k en fonction de v.
3) Montrer que l’onde électromagnétique résultante émise par l’ensemble de l’hologramme dans
la direction d’observation ???? peut s’écrire sous la forme :
???? ???????? ( ) 1 1 sin(????)
???? (????, ????) = ???? sinc ????(????) + sinc ????(????) + sinc ????(????) avec sinc(????) =
2 2 2 ????
????(????), ????(????) et ????(????) sont des fonct...
Physique : Evaluation de Fin de Semestre
Mardi 12 juin 2018 Durée : 3h00
Barème indicatif :
Le sujet est constitué de deux parties indépendantes
Barème indicatif sur 40:
Partie 1 : exercice 1 sur 15 points ; exercice 2 sur 10 points.
Partie 2 sur 15 points.
Document autorisé : une feuille de synthèse recto manuscrite originale
Calculatrice tout type non connectée (collège ou lycée) autorisée
Téléphone portable non autorisé
PARTIE 1 : Etude d’un microscope holographique numérique
Exercice 1 : Enregistrement d’un hologramme
Une photographie numérique classique est formée à partir de l’enregistrement, sur une matrice de
capteurs CCD, du signal lumineux reçu par chacun de ces capteurs considérés comme des détecteurs
quadratiques. Dans le cas des appareils numériques classiques, l’information contenue dans la phase
des rayons lumineux n’est donc pas enregistrée. Un dispositif holographique numérique permet
l’enregistrement de cette information de phase, et donc de retranscrire l’intégralité de l’information
portée par l’onde lumineuse reçue (d’où le terme d’hologramme, du grec holos qui signifie « en
entier »). Le dispositif étudié ici permet l’enregistrement d’hologrammes numériques pour
l’observation d’objets de petite taille (cellules, molécules) circulant dans un liquide.
Figure 1 : Vue d’ensemble du dispositif et coupe selon le plan (????????????).
Ce dispositif est constitué d’une plaque transparente, éclairée par une onde plane, progressive dans le
sens des ???? croissants, uniforme, harmonique, polarisée rectilignement selon Ox et en incidence
normale. Une partie du faisceau, appelée « faisceau d’observation », centré sur l’axe Oz, traverse
l’échantillon que l’on cherche à observer au sein d’un fluide circulant dans un canal prévu à cet effet.
Une autre partie du faisceau, appelée « faisceau de référence », traverse un réseau en transmission,
placé sur la plaque, et caractérisé par un pas « d ». Les deux sous-faisceaux se croisent par la suite
dans un plan appelé « plan d’observation ». L’image formée sur ce plan est ensuite agrandie par un
1
dispositif optique puis enregistrée par la matrice de capteurs CCD (ces deux dispositifs ne sont pas
étudiés ici).
Le centre du réseau est situé à la distance ???? de l’axe Oz (axe du faisceau d’observation). Le plan
d’observation est positionné à une hauteur ℎ de la plaque support. Un liquide d’indice ???? circule dans le
canal d’épaisseur ????. Le reste du dispositif est placé dans l’air que l’on prendra d’indice égal à 1.
1) Expliquer pourquoi le réseau donne lieu à une déviation du faisceau de référence, qui peut
donc croiser le faisceau d’observation.
2) Quel est le type d’interféromètre réalisé ici ?
Le dispositif a pour dimensions ℎ = 1 m et ???? = 400 mm et est éclairé par un faisceau
monochromatique dont la longueur d’onde est ???? = 633 nm dans le vide. On souhaite que le faisceau
d’observation croise le faisceau d’ordre 1 issu du réseau au point O. On considérera, pour simplifier le
problème, que la distance ℎ est suffisamment grande pour faire l’hypothèse que ce faisceau d’ordre 1
est une onde plane (cf. Figure 2).
3) Calculer l’angle de déviation nécessaire ???? = ???? pour que les deux faisceaux se croisent au
point O (cf. Figure 1). En déduire le pas du réseau et exprimer le nombre de fentes par
millimètres correspondant.
4) Exprimer la différence de chemin optique ???? entre les deux rayons qui interfèrent au point ????
en fonction de ????, ℎ, ???? et ???? et déterminer ???? pour que ???? = 0 en prenant ???? = 1,5. Dans toute la
suite du problème on considérera que cette condition sur e est vérifiée.
On considère donc les deux faisceaux (observation et référence) comme étant deux ondes planes et
uniformes dont les directions de propagation forment un angle ???? ( figure 2) :
Faisceau de référence Faisceau d’observation
Figure 2 : Intersection des deux sous-faisceaux, qui sont considérés comme deux ondes planes, dans le plan
d'observation.
5) Exprimer la différence de chemin optique ???? entre les deux ondes plane en un point quelconque
situé dans le plan d’observation en sachant qu’au point ????, ???? = 0.
6) Que va-t-on observer dans le plan d’observation ?
7) Donner toutes les caractéristiques de la figure qui résulte de la superposition de ces deux
faisceaux (on supposera qu’ils ont, au point considéré, la même intensité lumineuse ???? ).
2
8) Etablir, à l’aide d’une démonstration rigoureuse, que l’intensité lumineuse reçue dans le plan
d’observation dans ces conditions s’écrit sous la forme ????(????) = ???? 1 + cos Φ(y) . Exprimer
???? en fonction de ???? et Φ(y) en fonction de la distance interfrange ???? et de ????.
On suppose que des cellules sont présentes au sein du liquide qui remplit le canal. Celles-ci ont un
indice optique et un coefficient d’atténuation lumineuse différents de ceux du liquide.
9) En quoi cela va-t-il modifier la figure d’interférences obtenue grâce au dispositif ?
Exercice 2 : Observation d’un hologramme
L’image obtenue dans le plan d’observation grâce à la matrice de capteurs CCD peut ensuite être
imprimée sur un support transparent, que l’on appelle hologramme. Cet objet a une transparence qui
varie en fonction de l’intensité de l’onde qu’il a reçue pendant l’impression de l’image en chaque point
de sa surface de coordonnées (????, ????). Cette variation de transparence est associée à une « fonction de
transmission » ????(????, ????) (comprise entre 0 et 1) qui permet de calculer l’amplitude des rayons lumineux
transmis lorsqu’ils traversent l’hologramme éclairé par une onde plane (cette fonction vaut 1 dans les
zones parfaitement transparentes et 0 dans les zones parfaitement opaques).
Si on imprime la figure d’interférence obtenue dans le cas de l’exercice 1 (en absence de cellules dans
le liquide), on obtient un hologramme qui possède une fonction de transmission sinusoïdale de la
forme:
1 2???????? ???? ????
????(????) = 1 + cos pour − <????<+
2 ???? 2 2
L’image de l’hologramme (de largeur L et de hauteur H) et le profil de la fonction de transmission qui
lui est associé sont montrés sur la figure 3. En dehors de l’hologramme (???? < −????/2 ou ???? > ????/2) la
fonction de transmission est nulle (opaque). De plus la hauteur ???? de la zone de l’hologramme éclairée
est grande vis-à-vis de la longueur d’onde (les échelles ne sont pas respectées sur la figure).
a) ????
????(????)
1
b) ????
???? 0 ????
− ????
+
2 2
Figure 3 : a) Hologramme obtenu en imprimant la figure d’interférences de l’exercice 1 sur un support
transparent ; b) Fonction de transmission sinusoïdale associée à l’hologramme.
3
On éclaire cet hologramme à l’aide du même laser que celui utilisé précédemment, en incidence
normale, et on étudie le phénomène de diffraction engendré. Chaque élément de surface ???? ⋅ ????????
(surface d’Huygens élémentaire) peut être considéré comme une source secondaire de l’onde plane
incidente dont l’amplitude de l’onde réémise est égale à : ????(????) × ???? × ???? × ???????? (???? étant une constante
associée à l’amplitude de l’onde incidente).
1) Exprimer la différence de marche entre un rayon issu d’une fente élémentaire en ???? et le rayon
de référence issu du centre de l’hologramme en ???? = 0 dans une direction d’observation ????.
(Vous pourrez faire un petit schéma pour appuyer votre démonstration).
2) Donner l’expression complexe de l’onde émise par cette surface élémentaire dans la direction
d’observation. Dans cette expression, vous exprimerez le cosinus en fonction d’exponentielles
complexes (en utilisant la formule d’Euler), et le nombre d’onde k en fonction de v.
3) Montrer que l’onde électromagnétique résultante émise par l’ensemble de l’hologramme dans
la direction d’observation ???? peut s’écrire sous la forme :
???? ???????? ( ) 1 1 sin(????)
???? (????, ????) = ???? sinc ????(????) + sinc ????(????) + sinc ????(????) avec sinc(????) =
2 2 2 ????
????(????), ????(????) et ????(????) sont des fonct...












