Erreurs
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: mcboulba
Type : Classeur 3.6
Page(s) : 10
Taille Size: 514.83 Ko KB
Mis en ligne Uploaded: 29/01/2021 - 18:28:59
Uploadeur Uploader: mcboulba (Profil)
Téléchargements Downloads: 26
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2694661
Type : Classeur 3.6
Page(s) : 10
Taille Size: 514.83 Ko KB
Mis en ligne Uploaded: 29/01/2021 - 18:28:59
Uploadeur Uploader: mcboulba (Profil)
Téléchargements Downloads: 26
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2694661
Description
THEME1 - Chapitre3 : SLCI RECISION DES SLCI Lycée Jean Perrin PSI*
I - PROBLEMATIQUE
Sur un système linéaire asservi stable, plusieurs phénomènes sont à l’origine de la différence entre la consigne et la
réponse obtenue. Les inerties des solides en mouvement, les amortissements présents dans la chaîne d’énergie, les
frottements secs dans les liaisons. Afin de se conformer au cahier des charges lors de la conception d’un produit
industrialisé, il est indispensable de pourvoir :
• définir l’erreur entre la consigne et la réponse du système ;
• déterminer l’erreur en régime permanent ;
• étudier l’effet d’une perturbation physique s’exerçant sur le système.
Les perturbations sont des efforts s’opposant au fonctionnement du système. Elles influent sur la précision puisqu’elles
écartent la réponse de la consigne souhaitée.
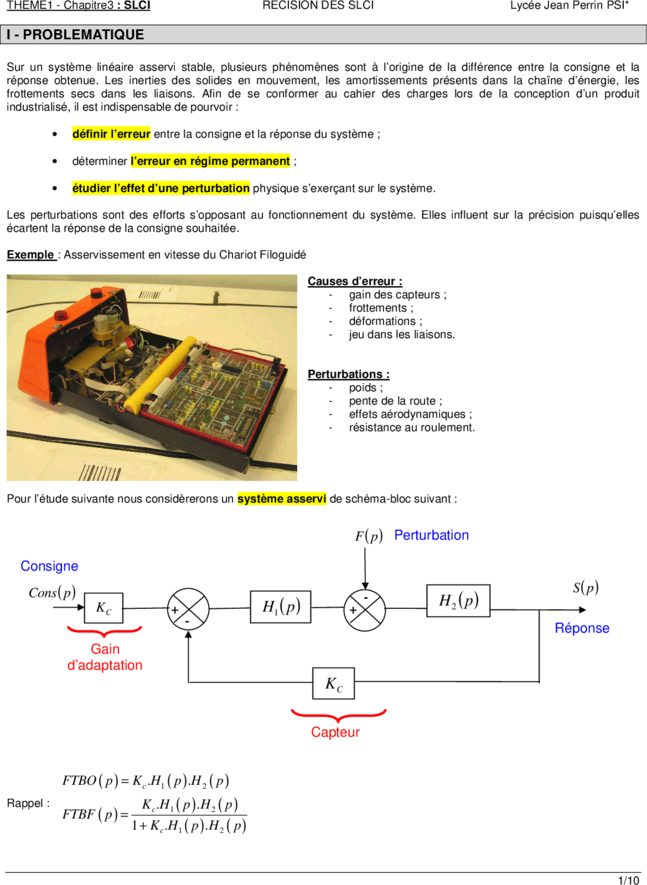
Exemple : Asservissement en vitesse du Chariot Filoguidé
Causes d’erreur :
- gain des capteurs ;
- frottements ;
- déformations ;
- jeu dans les liaisons.
Perturbations :
- poids ;
- pente de la route ;
- effets aérodynamiques ;
- résistance au roulement.
Pour l’étude suivante nous considèrerons un système asservi de schéma-bloc suivant :
F ( p ) Perturbation
Consigne
Cons ( p ) S ( p)
KC H1 ( p )
- H 2 ( p)
+ +
-
Réponse
Gain
d’adaptation
KC
Capteur
FTBO ( p ) = K c .H1 ( p ) .H 2 ( p )
Rappel : K c .H 1 ( p ) .H 2 ( p )
FTBF ( p ) =
1 + K c .H 1 ( p ) .H 2 ( p )
1/10
THEME1 - Chapitre3 : SLCI RECISION DES SLCI Lycée Jean Perrin PSI*
II - ETUDE DE L’ERREUR SANS PERTURBATION : Précision de l’asservissement
Plaçons dans le cas d’une perturbation nulle dans un premier temps. Le schéma bloc devient :
ε ( p)
Cons ( p ) S ( p)
KC + H1 ( p ) H 2 ( p)
-
KC
1. Erreur d’un système
• Définition 1 : l’erreur er (t ) d’un système est la différence entre la consigne cons (t ) et s (t ) :
er (t ) = cons (t ) − s (t ) NB : ε ( t ) = K c .er ( t )
ATTENTION s(t) et cons(t) ont même unité !!!
Cette erreur est instantanée, elle est différente à chaque instant.
S ( p) 0,7
Exemple : soit un système défini par sa FTBF : = . avec z<1. Ce système est soumis à une
Cons ( p ) 2z p2
1+ .p +
ω0 ωO 2
consigne échelon de hauteur A. Observons graphiquement l’erreur er (t ) de ce système.
e(t) s(t)
A
0,7.A
t
0
L’erreur instantanée n’est souvent pas observable par l’utilisateur car les temps de réponses de systèmes mécaniques
sont faibles. Cependant, il est intéressant de connaître la valeur de cette erreur en régime permanent, valeur observable
lors d’un asservissement de position par exemple.
Calcul de l’erreur :
2/10
THEME1 - Chapitre3 : SLCI RECISION DES SLCI Lycée Jean Perrin PSI*
1
E r ( p) = .Cons ( p )
1 + FTBO
La FTBO (fonction transfert en boucle ouverte) du système asservi peut être écrite sous forme canonique générale de la
manière suivante :
K 1 + a1 . p + .... + a n . p n
FTBO( p ) = . avec m > n
p α 1 + b1 . p + .... + bm . p m
K : gain statique de la FTBO
α ≥0 : classe du système
• Définition 2 :
1
la classe α d’un système asservi est le nombre d’intégrateur(s) présent(s) dans la boucle ouverte du système.
p
2. Erreur statique :
• Définition 3 : l’erreur statique E s d’un système est la valeur de l’erreur er (t ) en régime permanent :
Es = lim cons (t ) − s (t )
t →+∞
Le système asservi est soumis à une entrée échelon, rampe ou parabole. La consigne s’écrit donc dans le domaine de
Laplace :
A.u (t ) : Cons ( p ) =
A
Echelon ;
p
Rampe A.t.u (t ) : Cons ( p ) = 2 ;
A
p
Parabole A.t .u (t ) : Cons ( p ) = 3
2 A
p
Cons ( p ) =
A
La consigne peut être écrite sous la forme suivante : avec i = 1,2,3 .
pi
3/10
THEME1 - Chapitre3 : SLCI RECISION DES SLCI Lycée Jean Perrin PSI*
Calcul de l’erreur statique : Es = lim cons (t ) − s (t )
t →+∞
A 1
L’erreur statique d’un système sans perturbation est : E s = lim i −1
.
p →0 p 1+ K
pα
Nous pouvons dresser un tableau indiquant l’erreur statique en fonction de la classe α et du type de la consigne i .
Consigne
Echelon Rampe Parabole
A A A
p p2 p3
Classe α
α=0
α=1
α=2
4/10
THEME1 - Chapitre3 : SLCI RECISION DES SLCI Lycée Jean Perrin PSI*
Tableau des erreurs s...
I - PROBLEMATIQUE
Sur un système linéaire asservi stable, plusieurs phénomènes sont à l’origine de la différence entre la consigne et la
réponse obtenue. Les inerties des solides en mouvement, les amortissements présents dans la chaîne d’énergie, les
frottements secs dans les liaisons. Afin de se conformer au cahier des charges lors de la conception d’un produit
industrialisé, il est indispensable de pourvoir :
• définir l’erreur entre la consigne et la réponse du système ;
• déterminer l’erreur en régime permanent ;
• étudier l’effet d’une perturbation physique s’exerçant sur le système.
Les perturbations sont des efforts s’opposant au fonctionnement du système. Elles influent sur la précision puisqu’elles
écartent la réponse de la consigne souhaitée.
Exemple : Asservissement en vitesse du Chariot Filoguidé
Causes d’erreur :
- gain des capteurs ;
- frottements ;
- déformations ;
- jeu dans les liaisons.
Perturbations :
- poids ;
- pente de la route ;
- effets aérodynamiques ;
- résistance au roulement.
Pour l’étude suivante nous considèrerons un système asservi de schéma-bloc suivant :
F ( p ) Perturbation
Consigne
Cons ( p ) S ( p)
KC H1 ( p )
- H 2 ( p)
+ +
-
Réponse
Gain
d’adaptation
KC
Capteur
FTBO ( p ) = K c .H1 ( p ) .H 2 ( p )
Rappel : K c .H 1 ( p ) .H 2 ( p )
FTBF ( p ) =
1 + K c .H 1 ( p ) .H 2 ( p )
1/10
THEME1 - Chapitre3 : SLCI RECISION DES SLCI Lycée Jean Perrin PSI*
II - ETUDE DE L’ERREUR SANS PERTURBATION : Précision de l’asservissement
Plaçons dans le cas d’une perturbation nulle dans un premier temps. Le schéma bloc devient :
ε ( p)
Cons ( p ) S ( p)
KC + H1 ( p ) H 2 ( p)
-
KC
1. Erreur d’un système
• Définition 1 : l’erreur er (t ) d’un système est la différence entre la consigne cons (t ) et s (t ) :
er (t ) = cons (t ) − s (t ) NB : ε ( t ) = K c .er ( t )
ATTENTION s(t) et cons(t) ont même unité !!!
Cette erreur est instantanée, elle est différente à chaque instant.
S ( p) 0,7
Exemple : soit un système défini par sa FTBF : = . avec z<1. Ce système est soumis à une
Cons ( p ) 2z p2
1+ .p +
ω0 ωO 2
consigne échelon de hauteur A. Observons graphiquement l’erreur er (t ) de ce système.
e(t) s(t)
A
0,7.A
t
0
L’erreur instantanée n’est souvent pas observable par l’utilisateur car les temps de réponses de systèmes mécaniques
sont faibles. Cependant, il est intéressant de connaître la valeur de cette erreur en régime permanent, valeur observable
lors d’un asservissement de position par exemple.
Calcul de l’erreur :
2/10
THEME1 - Chapitre3 : SLCI RECISION DES SLCI Lycée Jean Perrin PSI*
1
E r ( p) = .Cons ( p )
1 + FTBO
La FTBO (fonction transfert en boucle ouverte) du système asservi peut être écrite sous forme canonique générale de la
manière suivante :
K 1 + a1 . p + .... + a n . p n
FTBO( p ) = . avec m > n
p α 1 + b1 . p + .... + bm . p m
K : gain statique de la FTBO
α ≥0 : classe du système
• Définition 2 :
1
la classe α d’un système asservi est le nombre d’intégrateur(s) présent(s) dans la boucle ouverte du système.
p
2. Erreur statique :
• Définition 3 : l’erreur statique E s d’un système est la valeur de l’erreur er (t ) en régime permanent :
Es = lim cons (t ) − s (t )
t →+∞
Le système asservi est soumis à une entrée échelon, rampe ou parabole. La consigne s’écrit donc dans le domaine de
Laplace :
A.u (t ) : Cons ( p ) =
A
Echelon ;
p
Rampe A.t.u (t ) : Cons ( p ) = 2 ;
A
p
Parabole A.t .u (t ) : Cons ( p ) = 3
2 A
p
Cons ( p ) =
A
La consigne peut être écrite sous la forme suivante : avec i = 1,2,3 .
pi
3/10
THEME1 - Chapitre3 : SLCI RECISION DES SLCI Lycée Jean Perrin PSI*
Calcul de l’erreur statique : Es = lim cons (t ) − s (t )
t →+∞
A 1
L’erreur statique d’un système sans perturbation est : E s = lim i −1
.
p →0 p 1+ K
pα
Nous pouvons dresser un tableau indiquant l’erreur statique en fonction de la classe α et du type de la consigne i .
Consigne
Echelon Rampe Parabole
A A A
p p2 p3
Classe α
α=0
α=1
α=2
4/10
THEME1 - Chapitre3 : SLCI RECISION DES SLCI Lycée Jean Perrin PSI*
Tableau des erreurs s...












