Stabilité
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: mcboulba
Type : Classeur 3.6
Page(s) : 10
Taille Size: 494.84 Ko KB
Mis en ligne Uploaded: 29/01/2021 - 18:27:00
Uploadeur Uploader: mcboulba (Profil)
Téléchargements Downloads: 25
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2694660
Type : Classeur 3.6
Page(s) : 10
Taille Size: 494.84 Ko KB
Mis en ligne Uploaded: 29/01/2021 - 18:27:00
Uploadeur Uploader: mcboulba (Profil)
Téléchargements Downloads: 25
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2694660
Description
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
STABILITE DES SYSTEMES ASSERVIS
1. L’instabilité ?
Du point de vue de l’utilisateur, l’instabilité d’un système se traduit par des oscillations aléatoires et longues. Par exemple,
pour un asservissement de position, un système instable n’atteindra pas une position fixe mais oscillera de manière
anarchique et incontrôlée autour d’une valeur.
Propriété :
D’un point de vue strictement théorique, un système est stable si et seulement si à une consigne bornée correspond une
réponse bornée elle aussi.
L’instabilité d’un système a des conséquences néfastes sur la précision et est la cause de graves dégradations dans les
liaisons mécaniques, l’ingénieur cherchera donc à s’éloigner le plus possible d’une situation instable en respectant des
« marges de stabilité » .
2. Critère de stabilité
Un système asservi est bouclé. Par conséquent, l’instabilité est due en fait à un « feedback », un « larsen » en quelque
sorte qui ne fait qu’augmenter. C’est cette situation qui est la cause de l’instabilité.
Pour déterminer un critère de stabilité, étudions l’évolution de l’écart ε (t ) . Si ε (t ) tend vers une valeur constante, à priori le
système est stable, si ε (t ) diverge, il y a de grandes chances que le système devienne instable.
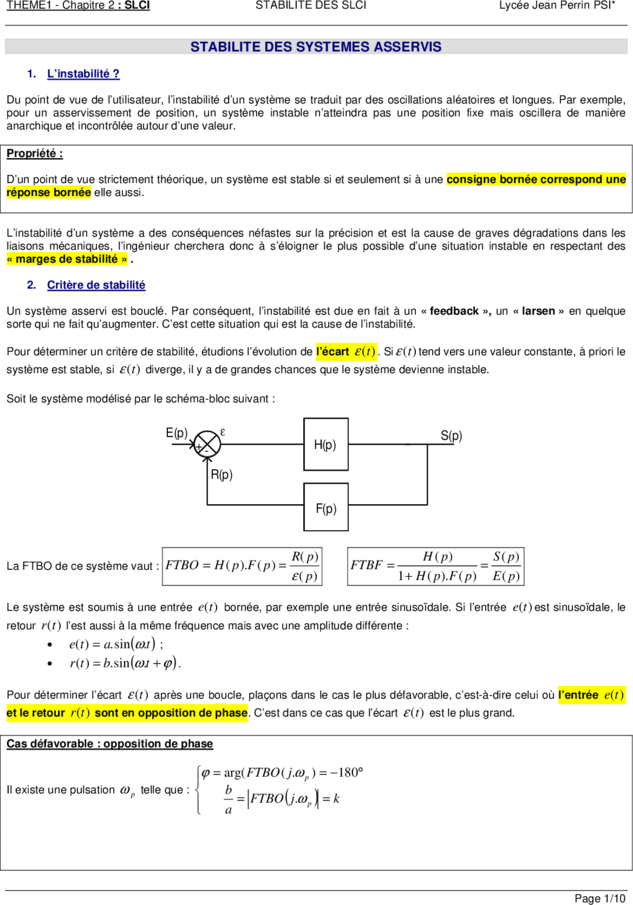
Soit le système modélisé par le schéma-bloc suivant :
E(p) ε S(p)
+- H(p)
R(p)
F(p)
R( p ) H ( p) S ( p)
La FTBO de ce système vaut : FTBO = H ( p ).F ( p ) = FTBF = =
ε ( p) 1 + H ( p ).F ( p ) E ( p )
Le système est soumis à une entrée e(t ) bornée, par exemple une entrée sinusoïdale. Si l’entrée e(t ) est sinusoïdale, le
retour r (t ) l’est aussi à la même fréquence mais avec une amplitude différente :
• e(t ) = a. sin (ω.t ) ;
• r (t ) = b. sin (ω.t + ϕ ) .
Pour déterminer l’écart ε (t ) après une boucle, plaçons dans le cas le plus défavorable, c’est-à-dire celui où l’entrée e(t )
et le retour r (t ) sont en opposition de phase. C’est dans ce cas que l’écart ε (t ) est le plus grand.
Cas défavorable : opposition de phase
ϕ = arg( FTBO ( j.ω p ) = −180°
ωp
= FTBO ( j.ω p ) = k
Il existe une pulsation telle que : b
a
Page 1/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
Tracé :
e(t) r1(t)
a
k.a
t
0
-k.a
-a
Après une boucle, ε1=e1-r1=a εi=ei-ri=ei-k (εi-1)
Après deux boucles, ε2=e2-r2=-a+(-k.a)=-a-k.a
….. ε3=e3-r3=a-(k.(-a-k.a))=a+k.a+k².a
n
Après n boucles, ε n = a. k i : divergent si k ≥ 1 et convergent si k < 1 .
i =0
Un critère de stabilité des systèmes asservis peut donc s’énoncer ainsi :
Critère de stabilité :
Lorsque le déphasage en boucle ouverte est de -180°, le système est stable si le module de la FTBO est strictement
inférieur à 1.
FTBO( j.ω p ) < 1
ωp arg( FTBO ( j.ω p )) = −180° stable si
Pour telle que
( )
20. log FTBO( j.ω p ) < 0
Pour appliquer ce critère de stabilité et évaluer la marge de stabilité, nous allons étudier en la FTBO du système asservi.
Nous disposerons d’une méthode graphique que nous allons présenter par la suite : l’analyse des diagrammes de Bode
Par ailleurs, il existe une méthode analytique basée sur l’analyse de la FTBF qui permet de conclure sur la stabilité : de
manière stricte (stable ou instable) sans pouvoir quantifier précisément la marge de stabilité vis-à-vis de l’instabilité. Il s’agit
de l’analyse des pôles de la FTBF ; nous la présenterons en fin de chapitre.
Page 2/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
3. Méthodes graphiques.
L’objectifs des méthodes graphiques est de déterminer d’une part si le système est stable ou pas mais l’étude va plus loin,
elle permet aussi de déterminer les « marges de stabilité ».
Ces marges n’ont de sens que lorsque LE SYSTEME VERIFIE LE CRITERE DE STABILITE.
• Marge de phase MP :
lorsque que le gain en dB est nul, la marge de phase notée MP représente le déphasage que peut prendre la FTBO
avant d’arriver à l’instabilité, soit -180°.
Pour ωC telle que 20. log FTBO(ω C ) = 0 dB , MP = 180° + arg(FTBO(ω C ))
• Marge de gain MG :
lorsque le déphasage de la FTBO est de -180°, la marge de gain MG représente le gain en dB restant avant d’atteindre
la limite de l’instabilité, soit 0 dB.
Pour ωP telle que arg( FTBO( j.ω p )) = −180° , MG = −20. log( FTBO(ω P ) )
a. Diagrammes de Bode.
L’étude de la stabilité se porte sur l’étude du déphasage et du gain AdB (ω ) de la FTBO.
On trace les diagrammes de gain et de déphasage de cette fonction transfert en boucle ouverte.
Marges de stabilité :
Marge de Gain :
Pour déterminer la marge de gain MG, on cherche ωp telle que le déphasage soit de -180°, en correspondance directe si
le gain AdB est <0 le système est stable, sinon il est instable.
Dans le cas d’un système stable, la marge de gain MG est l’écart avec le 0 dB.
Marge de Phase :
Dans le cas d’un système stable, pour déterminer la marge de phase MP, on cherche ω c telle que le gain AdB soit nul, en
correspondance directe la marge de phase MP est l’écart avec -180°.
NB : ces marges peuvent être, dans certains cas particuliers, infinies ou non définies
Page 3/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
Exemple 0 : Le système est stable, on cherche la marge de gain MG et la marge de phase MP graphiquement.
|HBO| (dB)
60
40
20
0
- 20
- 40
ω
ϕ (°) 0,01 0,1 1 10 ω
100
- 90
- 120
- 150
- 180
- 210
- 240
ω
0,01 0,1 1 10 100
Page 4/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
EXEMPLE 1 – cas stable
Page 5/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
EXEMPLE 2 – cas instable
Page 6/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
EXEMPLE 3 – détermination asymptotique des marges
Page 7/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
EXEMPLE 4 – marge non définie
Page 8/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
4. Méthode analytique : Analyse de pôles de la FTBF
En revenant à la définition de la stabilité théorique, un système est stable si à une entrée bornée il répond par une sortie
born?...
STABILITE DES SYSTEMES ASSERVIS
1. L’instabilité ?
Du point de vue de l’utilisateur, l’instabilité d’un système se traduit par des oscillations aléatoires et longues. Par exemple,
pour un asservissement de position, un système instable n’atteindra pas une position fixe mais oscillera de manière
anarchique et incontrôlée autour d’une valeur.
Propriété :
D’un point de vue strictement théorique, un système est stable si et seulement si à une consigne bornée correspond une
réponse bornée elle aussi.
L’instabilité d’un système a des conséquences néfastes sur la précision et est la cause de graves dégradations dans les
liaisons mécaniques, l’ingénieur cherchera donc à s’éloigner le plus possible d’une situation instable en respectant des
« marges de stabilité » .
2. Critère de stabilité
Un système asservi est bouclé. Par conséquent, l’instabilité est due en fait à un « feedback », un « larsen » en quelque
sorte qui ne fait qu’augmenter. C’est cette situation qui est la cause de l’instabilité.
Pour déterminer un critère de stabilité, étudions l’évolution de l’écart ε (t ) . Si ε (t ) tend vers une valeur constante, à priori le
système est stable, si ε (t ) diverge, il y a de grandes chances que le système devienne instable.
Soit le système modélisé par le schéma-bloc suivant :
E(p) ε S(p)
+- H(p)
R(p)
F(p)
R( p ) H ( p) S ( p)
La FTBO de ce système vaut : FTBO = H ( p ).F ( p ) = FTBF = =
ε ( p) 1 + H ( p ).F ( p ) E ( p )
Le système est soumis à une entrée e(t ) bornée, par exemple une entrée sinusoïdale. Si l’entrée e(t ) est sinusoïdale, le
retour r (t ) l’est aussi à la même fréquence mais avec une amplitude différente :
• e(t ) = a. sin (ω.t ) ;
• r (t ) = b. sin (ω.t + ϕ ) .
Pour déterminer l’écart ε (t ) après une boucle, plaçons dans le cas le plus défavorable, c’est-à-dire celui où l’entrée e(t )
et le retour r (t ) sont en opposition de phase. C’est dans ce cas que l’écart ε (t ) est le plus grand.
Cas défavorable : opposition de phase
ϕ = arg( FTBO ( j.ω p ) = −180°
ωp
= FTBO ( j.ω p ) = k
Il existe une pulsation telle que : b
a
Page 1/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
Tracé :
e(t) r1(t)
a
k.a
t
0
-k.a
-a
Après une boucle, ε1=e1-r1=a εi=ei-ri=ei-k (εi-1)
Après deux boucles, ε2=e2-r2=-a+(-k.a)=-a-k.a
….. ε3=e3-r3=a-(k.(-a-k.a))=a+k.a+k².a
n
Après n boucles, ε n = a. k i : divergent si k ≥ 1 et convergent si k < 1 .
i =0
Un critère de stabilité des systèmes asservis peut donc s’énoncer ainsi :
Critère de stabilité :
Lorsque le déphasage en boucle ouverte est de -180°, le système est stable si le module de la FTBO est strictement
inférieur à 1.
FTBO( j.ω p ) < 1
ωp arg( FTBO ( j.ω p )) = −180° stable si
Pour telle que
( )
20. log FTBO( j.ω p ) < 0
Pour appliquer ce critère de stabilité et évaluer la marge de stabilité, nous allons étudier en la FTBO du système asservi.
Nous disposerons d’une méthode graphique que nous allons présenter par la suite : l’analyse des diagrammes de Bode
Par ailleurs, il existe une méthode analytique basée sur l’analyse de la FTBF qui permet de conclure sur la stabilité : de
manière stricte (stable ou instable) sans pouvoir quantifier précisément la marge de stabilité vis-à-vis de l’instabilité. Il s’agit
de l’analyse des pôles de la FTBF ; nous la présenterons en fin de chapitre.
Page 2/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
3. Méthodes graphiques.
L’objectifs des méthodes graphiques est de déterminer d’une part si le système est stable ou pas mais l’étude va plus loin,
elle permet aussi de déterminer les « marges de stabilité ».
Ces marges n’ont de sens que lorsque LE SYSTEME VERIFIE LE CRITERE DE STABILITE.
• Marge de phase MP :
lorsque que le gain en dB est nul, la marge de phase notée MP représente le déphasage que peut prendre la FTBO
avant d’arriver à l’instabilité, soit -180°.
Pour ωC telle que 20. log FTBO(ω C ) = 0 dB , MP = 180° + arg(FTBO(ω C ))
• Marge de gain MG :
lorsque le déphasage de la FTBO est de -180°, la marge de gain MG représente le gain en dB restant avant d’atteindre
la limite de l’instabilité, soit 0 dB.
Pour ωP telle que arg( FTBO( j.ω p )) = −180° , MG = −20. log( FTBO(ω P ) )
a. Diagrammes de Bode.
L’étude de la stabilité se porte sur l’étude du déphasage et du gain AdB (ω ) de la FTBO.
On trace les diagrammes de gain et de déphasage de cette fonction transfert en boucle ouverte.
Marges de stabilité :
Marge de Gain :
Pour déterminer la marge de gain MG, on cherche ωp telle que le déphasage soit de -180°, en correspondance directe si
le gain AdB est <0 le système est stable, sinon il est instable.
Dans le cas d’un système stable, la marge de gain MG est l’écart avec le 0 dB.
Marge de Phase :
Dans le cas d’un système stable, pour déterminer la marge de phase MP, on cherche ω c telle que le gain AdB soit nul, en
correspondance directe la marge de phase MP est l’écart avec -180°.
NB : ces marges peuvent être, dans certains cas particuliers, infinies ou non définies
Page 3/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
Exemple 0 : Le système est stable, on cherche la marge de gain MG et la marge de phase MP graphiquement.
|HBO| (dB)
60
40
20
0
- 20
- 40
ω
ϕ (°) 0,01 0,1 1 10 ω
100
- 90
- 120
- 150
- 180
- 210
- 240
ω
0,01 0,1 1 10 100
Page 4/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
EXEMPLE 1 – cas stable
Page 5/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
EXEMPLE 2 – cas instable
Page 6/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
EXEMPLE 3 – détermination asymptotique des marges
Page 7/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
EXEMPLE 4 – marge non définie
Page 8/10
THEME1 - Chapitre 2 : SLCI STABILITE DES SLCI Lycée Jean Perrin PSI*
4. Méthode analytique : Analyse de pôles de la FTBF
En revenant à la définition de la stabilité théorique, un système est stable si à une entrée bornée il répond par une sortie
born?...












