Réponse fréquentielle
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: mcboulba
Type : Classeur 3.6
Page(s) : 13
Taille Size: 486.78 Ko KB
Mis en ligne Uploaded: 29/01/2021 - 18:24:56
Uploadeur Uploader: mcboulba (Profil)
Téléchargements Downloads: 24
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2694658
Type : Classeur 3.6
Page(s) : 13
Taille Size: 486.78 Ko KB
Mis en ligne Uploaded: 29/01/2021 - 18:24:56
Uploadeur Uploader: mcboulba (Profil)
Téléchargements Downloads: 24
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2694658
Description
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
Pour l’étude fréquentielle des systèmes asservis, nous utiliserons les diagrammes de Bode de gain et de Phase.
L’objectif de ce cours est d’analyser la réponse fréquentielle d’un système linéaire à l’aide du tracé asymptotique et réel
des diagrammes de Bode dans le but d’étudier sa stabilité dans un prochain chapitre
I. ETUDE FREQUENTIELLE : RAPPEL
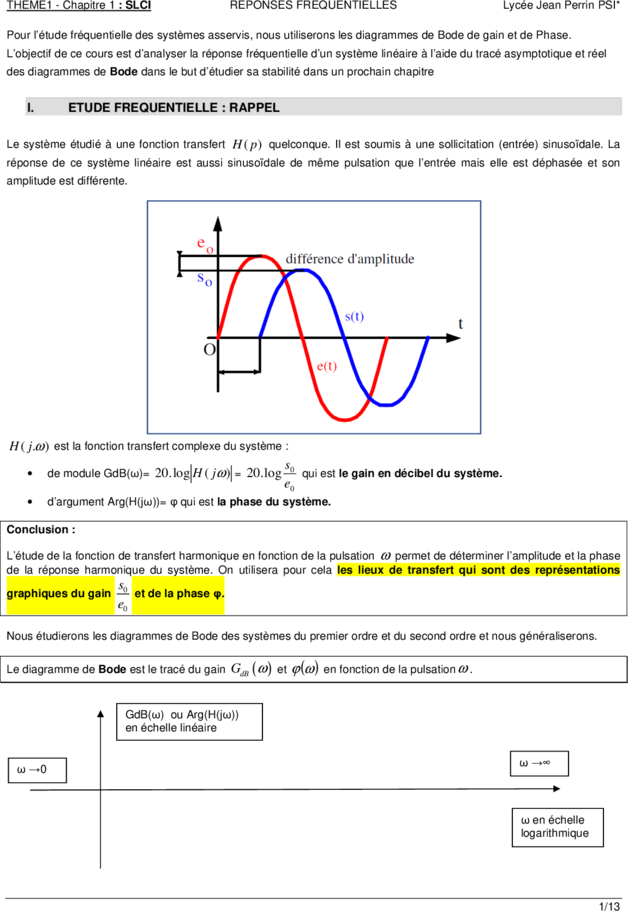
Le système étudié à une fonction transfert H ( p ) quelconque. Il est soumis à une sollicitation (entrée) sinusoïdale. La
réponse de ce système linéaire est aussi sinusoïdale de même pulsation que l’entrée mais elle est déphasée et son
amplitude est différente.
H ( j.ω ) est la fonction transfert complexe du système :
s
• de module GdB(ω)= 20. log H ( jω ) = 20. log 0 qui est le gain en décibel du système.
e0
• d’argument Arg(H(jω))= φ qui est la phase du système.
Conclusion :
L’étude de la fonction de transfert harmonique en fonction de la pulsation ω permet de déterminer l’amplitude et la phase
de la réponse harmonique du système. On utilisera pour cela les lieux de transfert qui sont des représentations
s0
graphiques du gain et de la phase φ.
e0
Nous étudierons les diagrammes de Bode des systèmes du premier ordre et du second ordre et nous généraliserons.
Le diagramme de Bode est le tracé du gain GdB (ω ) et ϕ (ω ) en fonction de la pulsation ω .
GdB(ω) ou Arg(H(jω))
en échelle linéaire
ω →∞
ω →0
ω en échelle
logarithmique
1/13
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
II. DIAGRAMME DE BODE pour les systèmes du 1er et 2d ordre
1. Système du premier ordre
Soit un système du premier ordre de fonction transfert :
E(p) K S(p)
1+τ.p
Système du premier ordre
Diagrammes de Bode
Gain
Phase
2/13
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
2. Système du deuxième ordre
Soit un système du second ordre de fonction transfert :
E(p) K S(p)
2ξ p 2
1+ .p +
ω0 ω0 2
système du second ordre
Diagrammes de Bode
Gain
Phase
3/13
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
Diagramme de Bode réel en fonction du coefficient d’amortissement :
0,1 1 10 100
10
GdB(ω) ω
5
0
-5
-10 0,01
0,1
-15 0,4
Coefficient
0,7
-20
d'amortissement ξ
1
1,3
-25
2
-30
-35
0,1 1 10 100 1000
20
ϕ(ω)° ω
0
-20
-40
-60
Coefficient
-80 d'amortissement ξ
-100 0,01
0,1
-120
0,4
0,7
-140
1
1,3
-160
2
-180
-200
Evolution de la réponse fréquentielle d’un système du second ordre avec l’amortissement ξ
(ω0=10 rad/s, K=1)
4/13
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
Récapitulatif temporel/fréquentiel pour les systèmes du second ordre
PSEUDO PERIODIQUE s(t) CRITIQUE
DOMAINE TEMPOREL
s(t) t
s(t) APERIODIQUE
t
2 t
REPONSE + RAPIDE 2
ξ coefficient
d’amortissement
0,7 1
BODE REELS
DOMAINE FREQUENTIEL
AdB AdB
ω ω
RESONANCE NON RESONANCE
BODE ASYMPTOTIQUES
G( ω ) dB G( ω ) dB
ξ <1 ξ >1
ω0 ω ω1 ω0 ω2 ω
K dB K dB
−40 dB/dec −40 dB/dec
ϕ ω ϕ ω
-90° -90°
-180° -180°
2
2
ξ
0,7 1
5/13
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
III. ANALYSE DES SYSTEMES ELEMENTAIRES
1. Gain pur : H( jω) = K GdB
20 log K
gain :G dB = 20 log K ω
phase : ϕ = 0°
ϕ°
ω
BODE
2. Dérivateur pur : H( jω) = jKω
gain :G dB = 20 log K + 20 log ω GdB
(+1)
phase : ϕ = +90° 1 ω
...
Pour l’étude fréquentielle des systèmes asservis, nous utiliserons les diagrammes de Bode de gain et de Phase.
L’objectif de ce cours est d’analyser la réponse fréquentielle d’un système linéaire à l’aide du tracé asymptotique et réel
des diagrammes de Bode dans le but d’étudier sa stabilité dans un prochain chapitre
I. ETUDE FREQUENTIELLE : RAPPEL
Le système étudié à une fonction transfert H ( p ) quelconque. Il est soumis à une sollicitation (entrée) sinusoïdale. La
réponse de ce système linéaire est aussi sinusoïdale de même pulsation que l’entrée mais elle est déphasée et son
amplitude est différente.
H ( j.ω ) est la fonction transfert complexe du système :
s
• de module GdB(ω)= 20. log H ( jω ) = 20. log 0 qui est le gain en décibel du système.
e0
• d’argument Arg(H(jω))= φ qui est la phase du système.
Conclusion :
L’étude de la fonction de transfert harmonique en fonction de la pulsation ω permet de déterminer l’amplitude et la phase
de la réponse harmonique du système. On utilisera pour cela les lieux de transfert qui sont des représentations
s0
graphiques du gain et de la phase φ.
e0
Nous étudierons les diagrammes de Bode des systèmes du premier ordre et du second ordre et nous généraliserons.
Le diagramme de Bode est le tracé du gain GdB (ω ) et ϕ (ω ) en fonction de la pulsation ω .
GdB(ω) ou Arg(H(jω))
en échelle linéaire
ω →∞
ω →0
ω en échelle
logarithmique
1/13
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
II. DIAGRAMME DE BODE pour les systèmes du 1er et 2d ordre
1. Système du premier ordre
Soit un système du premier ordre de fonction transfert :
E(p) K S(p)
1+τ.p
Système du premier ordre
Diagrammes de Bode
Gain
Phase
2/13
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
2. Système du deuxième ordre
Soit un système du second ordre de fonction transfert :
E(p) K S(p)
2ξ p 2
1+ .p +
ω0 ω0 2
système du second ordre
Diagrammes de Bode
Gain
Phase
3/13
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
Diagramme de Bode réel en fonction du coefficient d’amortissement :
0,1 1 10 100
10
GdB(ω) ω
5
0
-5
-10 0,01
0,1
-15 0,4
Coefficient
0,7
-20
d'amortissement ξ
1
1,3
-25
2
-30
-35
0,1 1 10 100 1000
20
ϕ(ω)° ω
0
-20
-40
-60
Coefficient
-80 d'amortissement ξ
-100 0,01
0,1
-120
0,4
0,7
-140
1
1,3
-160
2
-180
-200
Evolution de la réponse fréquentielle d’un système du second ordre avec l’amortissement ξ
(ω0=10 rad/s, K=1)
4/13
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
Récapitulatif temporel/fréquentiel pour les systèmes du second ordre
PSEUDO PERIODIQUE s(t) CRITIQUE
DOMAINE TEMPOREL
s(t) t
s(t) APERIODIQUE
t
2 t
REPONSE + RAPIDE 2
ξ coefficient
d’amortissement
0,7 1
BODE REELS
DOMAINE FREQUENTIEL
AdB AdB
ω ω
RESONANCE NON RESONANCE
BODE ASYMPTOTIQUES
G( ω ) dB G( ω ) dB
ξ <1 ξ >1
ω0 ω ω1 ω0 ω2 ω
K dB K dB
−40 dB/dec −40 dB/dec
ϕ ω ϕ ω
-90° -90°
-180° -180°
2
2
ξ
0,7 1
5/13
THEME1 - Chapitre 1 : SLCI REPONSES FREQUENTIELLES Lycée Jean Perrin PSI*
III. ANALYSE DES SYSTEMES ELEMENTAIRES
1. Gain pur : H( jω) = K GdB
20 log K
gain :G dB = 20 log K ω
phase : ϕ = 0°
ϕ°
ω
BODE
2. Dérivateur pur : H( jω) = jKω
gain :G dB = 20 log K + 20 log ω GdB
(+1)
phase : ϕ = +90° 1 ω
...












