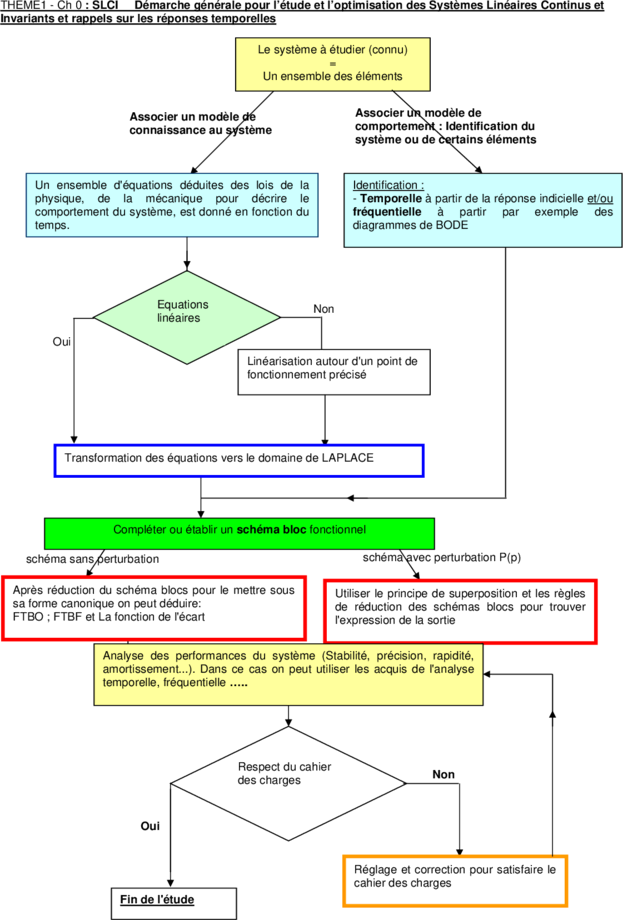
THEME1 - Ch 0 : SLCI Démarche générale pour l’étude et l’optimisation des Systèmes Linéaires Continus et
Invariants et rappels sur les réponses temporelles

Le système à étudier (connu)
=
Un ensemble des éléments


Associer un modèle de Associer un modèle de
connaissance au système comportement : Identification du
système ou de certains éléments


Un ensemble d'équations déduites des lois de la Identification :
physique, de la mécanique pour décrire le - Temporelle à partir de la réponse indicielle et/ou
comportement du système, est donné en fonction du fréquentielle à partir par exemple des
temps. diagrammes de BODE




Equations Non
linéaires

Oui
Linéarisation autour d'un point de
fonctionnement précisé




Transformation des équations vers le domaine de LAPLACE




Compléter ou établir un schéma bloc fonctionnel

schéma sans perturbation schéma avec perturbation P(p)

Après réduction du schéma blocs pour le mettre sous Utiliser le principe de superposition et les règles
sa forme canonique on peut déduire: de réduction des schémas blocs pour trouver
FTBO ; FTBF et La fonction de l'écart l'expression de la sortie


Analyse des performances du système (Stabilité, précision, rapidité,
amortissement...). Dans ce cas on peut utiliser les acquis de l'analyse
temporelle, fréquentielle …..




Respect du cahier
Non
des charges



Oui


Réglage et correction pour satisfaire le
cahier des charges
Fin de l'étude
 Propriétés de la transformée de Laplace


1) Unicité
À une correspond une unique, et inversement.

2) Linéarité



3) Théorème du retard


4) Théorème de dérivation




5) Théorème d'intégration




6) Théorème de la valeur initiale


7) Théorème de la valeur finale
 Rappel : la réponse indicielle est la
réponse à l’échelon ; on prendra ici un
échelon unitaire

s(t ) = K (1 − e−t /τ ) pour t ≥ 0




NB : si l’échelon est d’amplitude A, la réponse est multipliée par A s (t ) = AK (1 − e − t /τ ) pour t ≥ 0
 EXEMPLE : SYSTEMES DU 1er ordre

Calcul et tracé de réponse
S ( p) 20
H ( p) = =
E ( p) 5 + p
1. Sachant ici que e(t) est l’echelon d’amplitude 5, combien vaut :

E ( p) = s (t ) =


2. Tracer la réponse s(t) à l’échelon d’amplitude 5 - Allure et points caractéristiques (valeur finale, T5%,
tangente en 0, temps caractéristique…) – Vous respecterez scrupuleusement votre choix d’échelle.




Identification :

s (t )




e (t )




1. A l’aide d’une identification graphique , combien vaut :



E ( p) = H ( p) =

s (t ) =
  −πξ 
 
 1−ξ 2  D1
D1% = e  
=
K




NB : si l’échelon est d’amplitude A, la réponse est multipliée par A
ξ≤1 ξ≥1
1er Dépassement
EXEMPLE : SYSTEMES DU 2d ordre

Calcul et tracé de réponse
3
S ( p) 2
H ( p) = =
E ( p) 1 + p + p 2
1. Donner ξ et ω0 . En déduire D1 (pour l’échelon d’amplitude 2 ) et T.



Pulsation propre ω0 =


Coefficient d’amortissement : ξ=

E ( p) =


D1 =



D1 %=



T=



2. Tracer la réponse s(t) à l’échelon d’amplitude 2 - Allure et points caractéristiques (valeur finale, T5%,
tangente en 0, temps caractéristique…) – Vous respecterez scrupuleusement votre choix d’échelle.
Identification




1. A l’aide d’une identification graphique , combien vaut :



E ( p) =




D1 =



Coefficient d’amortissement : ξ=


T=




Pulsation propre ω0 =




H ( p) =