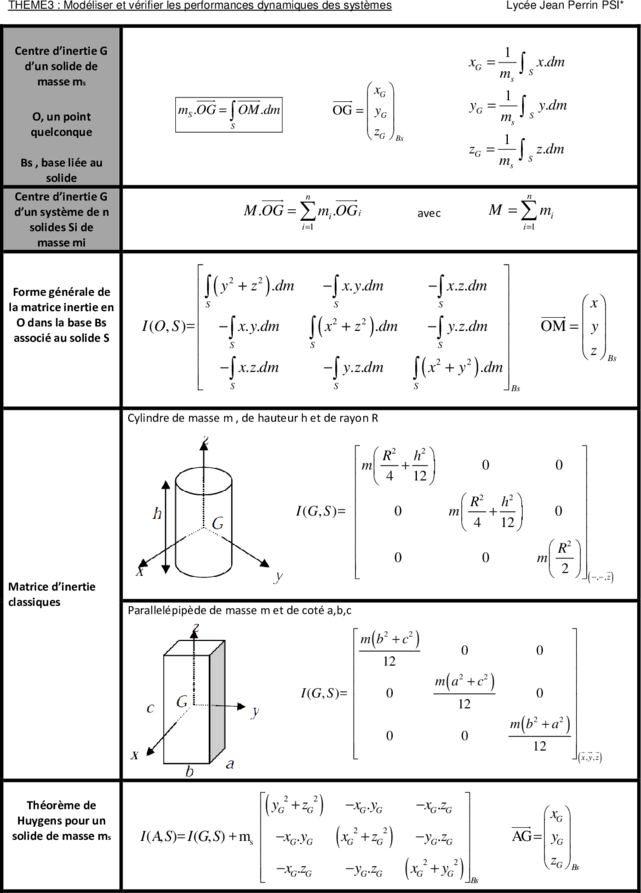
THEME3 : Modéliser et vérifier les performances dynamiques des systèmes Lycée Jean Perrin PSI*



Centre d’inertie G 1
d’un solide de xG =
ms ∫ S
x.dm
masse ms
 xG  1
 
O, un point
mS .OG = ∫ OM .dm OG =  yG  yG =
ms ∫ S
y.dm
S z 
quelconque  G  Bs 1
Bs , base liée au
zG =
ms ∫ S
z.dm
solide
Centre d’inertie G n n
d’un système de n M .OG = ∑ mi .OG i avec M = ∑ mi
solides Si de i =1 i =1
masse mi

 
 ∫ ( y + z ) .dm − ∫ x. y.dm − ∫ x.z.dm
2 2
Forme générale de 
la matrice inertie en S S S  x
∫S ( x + z ) .dm −∫S y.z.dm 
 
O dans la base Bs I (O, S )=  − ∫ x. y.dm 2 2  OM =  y 
associé au solide S
 S
 z 
  Bs
 − x.z.dm
 ∫S − ∫ y.z.dm ∫ ( x + y ).dm 
2 2

S S  Bs

Cylindre de masse m , de hauteur h et de rayon R

  R 2 h2  
m  +  0 0 
  4 12  
 R 2
h 
2 
I (G , S )=  0 m +  0 
  4 12  
 
  R2 
 0 0 m 
  2   ( − , − , z )
Matrice d’inertie
classiques
Parallelépipède de masse m et de coté a,b,c

 m ( b2 + c2 ) 
 0 0 
 12 
 m ( a 2 + c2 ) 
I (G, S )=  0 0 
 12 
 
 m ( b2 + a2 ) 
 0 0 
 12  ( x , y , z )


Théorème de
Huygens pour un
(
 yG2 + zG2

) −xG .yG −xG .zG 
  xG 
solide de masse ms I ( A, S)= I (G, S) + ms  −xG .yG
 (xG
2
+ zG
2
) −yG .zG 

 
AG =  yG 
z 

 −xG .zG −yG.zG ( xG + yG 
2
)
2 
Bs
 G Bs
  Rc ( S/R ) = V ( M,S/R ) .dm 
 ∫ 
Torseur cinétique {C ( S/R )}A =  S

σ ( A, S/R ) = ∫ S AM ∧ V ( M,S/R ) .dm 
A

Rc ( S/R ) = ms .V ( G , S/R )
Résultante
cinétique


Moment cinétique σ ( A, S/R ) = I ( A, S ).Ω ( S/R ) + ms . AG ∧ V ( A, S/R )...