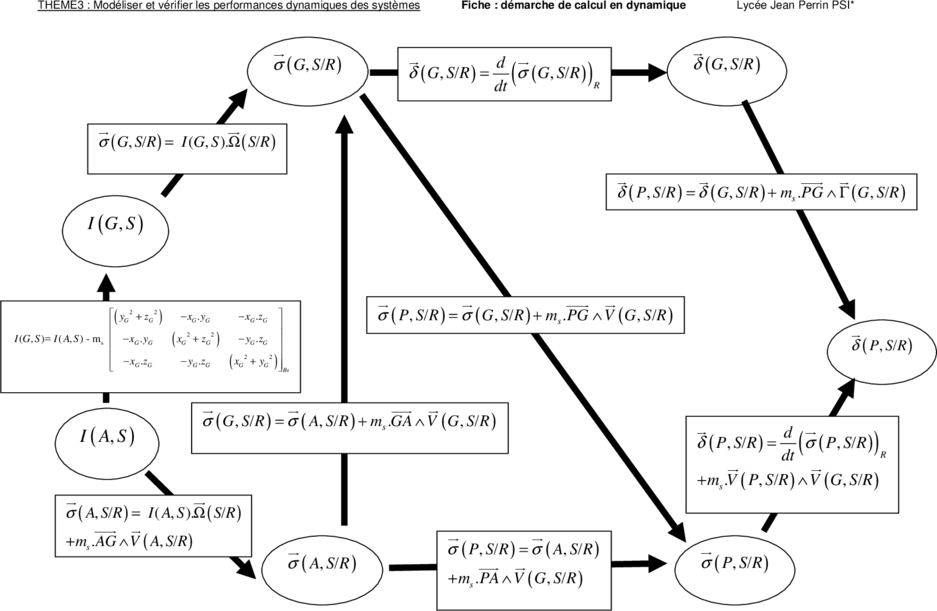
THEME3 : Modéliser et vérifier les performances dynamiques des systèmes Fiche : démarche de calcul en dynamique Lycée Jean Perrin PSI*




σ ( G , S /R ) δ ( G , S/ R )
δ ( G , S/R ) =
d
dt
(
σ ( G , S/ R ) ) R




σ ( G, S/R ) = I (G, S ).Ω ( S/R )


δ ( P , S/R ) = δ ( G , S/R ) + ms .PG ∧ Γ ( G , S/R )
I ( G, S )




(
 yG 2 + zG 2

) − xG . yG − xG .zG 

σ ( P , S/R ) = σ ( G , S/R ) + ms .PG ∧ V ( G , S/R )
I (G , S )= I ( A, S ) - ms  − xG . yG
 (x
G
2
+ zG
2
) − yG . zG 
 δ ( P , S /R )


− xG . zG − yG .zG (x
G
2
+ yG
2
) 
 Bs




σ ( G , S/R ) = σ ( A, S/R ) + ms .GA ∧ V ( G , S/R )
I ( A, S ) δ ( P , S/ R ) =
d
(σ ( P , S/ R ))
dt R

+ ms .V ( P, S/R ) ∧ V ( G , S/R )
σ ( A, S/R ) = I ( A, S ).Ω ( S/R )
+ ms . AG ∧ V ( A, S/R )
σ ( P , S/R ) = σ ( A, S/R )
σ ( A, S/R ) σ ( P , S/ R )
+ ms .PA ∧ V ( G , S/R )