Schéma bloc
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: mcboulba
Type : Classeur 3.6
Page(s) : 3
Taille Size: 186.08 Ko KB
Mis en ligne Uploaded: 29/01/2021 - 18:03:56
Uploadeur Uploader: mcboulba (Profil)
Téléchargements Downloads: 27
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2694643
Type : Classeur 3.6
Page(s) : 3
Taille Size: 186.08 Ko KB
Mis en ligne Uploaded: 29/01/2021 - 18:03:56
Uploadeur Uploader: mcboulba (Profil)
Téléchargements Downloads: 27
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2694643
Description
Comportement des SLCI - Chapitre 3 PCSI – Lycée Jean Perrin
M
anipulation des schémas-blocs
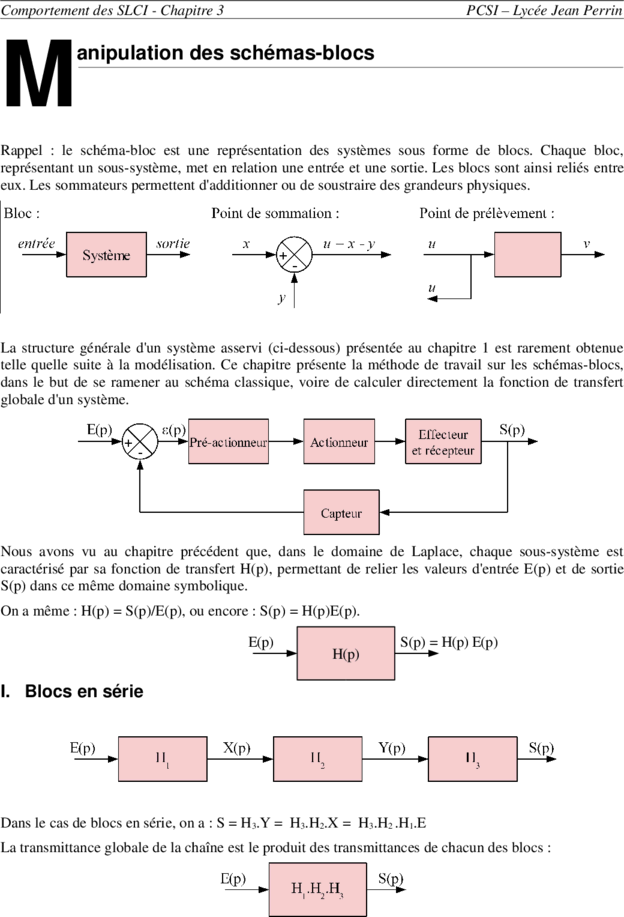
Rappel : le schéma-bloc est une représentation des systèmes sous forme de blocs. Chaque bloc,
représentant un sous-système, met en relation une entrée et une sortie. Les blocs sont ainsi reliés entre
eux. Les sommateurs permettent d'additionner ou de soustraire des grandeurs physiques.
La structure générale d'un système asservi (ci-dessous) présentée au chapitre 1 est rarement obtenue
telle quelle suite à la modélisation. Ce chapitre présente la méthode de travail sur les schémas-blocs,
dans le but de se ramener au schéma classique, voire de calculer directement la fonction de transfert
globale d'un système.
Nous avons vu au chapitre précédent que, dans le domaine de Laplace, chaque sous-système est
caractérisé par sa fonction de transfert H(p), permettant de relier les valeurs d'entrée E(p) et de sortie
S(p) dans ce même domaine symbolique.
On a même : H(p) = S(p)/E(p), ou encore : S(p) = H(p)E(p).
E(p) S(p) = H(p) E(p)
H(p)
I. Blocs en série
Dans le cas de blocs en série, on a : S = H3.Y = H3.H2.X = H3.H2 .H1.E
La transmittance globale de la chaîne est le produit des transmittances de chacun des blocs :
II. Blocs en parallèle
=
On a : S(p) = H1.E + H2 .E = (H1 + H2 ).E
On peut donc remplacer ces deux blocs et le sommateur par un seul bloc dont la fonction de transfert
est la somme de H1(p) et H2(p).
III. Boucle fermée
E(p) ε(p) S(p)
+ H
-
=
Y(p)
G
On a : Y = G.S ; ε=E–Y ; S = H. ε
soit S = H.(E – Y) = H.(E – G.S) donc : S.(1 + GH) = H.E
H p
soit enfin : S p= ⋅E p
1H p ⋅G p
IV. Déplacement d'un point de prélèvement
1) Déplacement vers la droite
E S
H =
E
Comme : E = S/H , lors du déplacement vers la droite d'un point de prélèvement (par-dessus un bloc
H), il faut rajouter après le point un bloc de fonction de transfert H' = 1/H.
2) Déplacement vers la gauche
E S
H =
S
Comme : S = HE , lors du déplacement vers la gauche d'un point de prélèvement (par-dessus un bloc
H), il faut rajouter après le prélèvement un bloc de fonction de transfert H.
Schémas-Blocs 2
V. Fonction de transfert en boucle ouverte / en boucle fermée
Soit le schéma fonctionnel suivant :
E ε S
• H est appelée transmittance de la chaîne directe. + H
-
• G est la fonction de transfert de la boucle de retour R
G
H p
D'après le paragraphe III : S p= ⋅E p .
1 H p⋅G p
H p
• La fonction de transfert est appelée fonction de transfert en boucle fermée
1 H p ⋅G p
(FTBF) du système.
• H.G est la fonction de transfert en boucle ouverte (FTBO) du système.
On a : R = HGε. La FTBO Correspond au bout de la chaîne si
E ε S
on ouvre le schéma au niveau du comparateur. + H
-
La FTBO est égale au produit des fonctions de transfert de
chaque bloc de la boucle.
La fonction de transfert en boucle ouverte est utilisée pour R
G
déterminer les conditions de stabilité et de précision d’un
système asservi (cours de 2ème année).
Remarque : cas du retour unitaire
Le système est à retour unitaire si la fonction de transfert de la boucle de retour vaut 1. On peut, dans ce
cas, comparer directement les valeurs d'entrée et de sortie (même grandeur physique).
E ε S
+ H
-
R
H p
Alors, la FTBO est égale à la fonction de transfert de la chaîne directe H et la FTBF vaut : .
1H p
Schémas-Blocs 3
M
anipulation des schémas-blocs
Rappel : le schéma-bloc est une représentation des systèmes sous forme de blocs. Chaque bloc,
représentant un sous-système, met en relation une entrée et une sortie. Les blocs sont ainsi reliés entre
eux. Les sommateurs permettent d'additionner ou de soustraire des grandeurs physiques.
La structure générale d'un système asservi (ci-dessous) présentée au chapitre 1 est rarement obtenue
telle quelle suite à la modélisation. Ce chapitre présente la méthode de travail sur les schémas-blocs,
dans le but de se ramener au schéma classique, voire de calculer directement la fonction de transfert
globale d'un système.
Nous avons vu au chapitre précédent que, dans le domaine de Laplace, chaque sous-système est
caractérisé par sa fonction de transfert H(p), permettant de relier les valeurs d'entrée E(p) et de sortie
S(p) dans ce même domaine symbolique.
On a même : H(p) = S(p)/E(p), ou encore : S(p) = H(p)E(p).
E(p) S(p) = H(p) E(p)
H(p)
I. Blocs en série
Dans le cas de blocs en série, on a : S = H3.Y = H3.H2.X = H3.H2 .H1.E
La transmittance globale de la chaîne est le produit des transmittances de chacun des blocs :
II. Blocs en parallèle
=
On a : S(p) = H1.E + H2 .E = (H1 + H2 ).E
On peut donc remplacer ces deux blocs et le sommateur par un seul bloc dont la fonction de transfert
est la somme de H1(p) et H2(p).
III. Boucle fermée
E(p) ε(p) S(p)
+ H
-
=
Y(p)
G
On a : Y = G.S ; ε=E–Y ; S = H. ε
soit S = H.(E – Y) = H.(E – G.S) donc : S.(1 + GH) = H.E
H p
soit enfin : S p= ⋅E p
1H p ⋅G p
IV. Déplacement d'un point de prélèvement
1) Déplacement vers la droite
E S
H =
E
Comme : E = S/H , lors du déplacement vers la droite d'un point de prélèvement (par-dessus un bloc
H), il faut rajouter après le point un bloc de fonction de transfert H' = 1/H.
2) Déplacement vers la gauche
E S
H =
S
Comme : S = HE , lors du déplacement vers la gauche d'un point de prélèvement (par-dessus un bloc
H), il faut rajouter après le prélèvement un bloc de fonction de transfert H.
Schémas-Blocs 2
V. Fonction de transfert en boucle ouverte / en boucle fermée
Soit le schéma fonctionnel suivant :
E ε S
• H est appelée transmittance de la chaîne directe. + H
-
• G est la fonction de transfert de la boucle de retour R
G
H p
D'après le paragraphe III : S p= ⋅E p .
1 H p⋅G p
H p
• La fonction de transfert est appelée fonction de transfert en boucle fermée
1 H p ⋅G p
(FTBF) du système.
• H.G est la fonction de transfert en boucle ouverte (FTBO) du système.
On a : R = HGε. La FTBO Correspond au bout de la chaîne si
E ε S
on ouvre le schéma au niveau du comparateur. + H
-
La FTBO est égale au produit des fonctions de transfert de
chaque bloc de la boucle.
La fonction de transfert en boucle ouverte est utilisée pour R
G
déterminer les conditions de stabilité et de précision d’un
système asservi (cours de 2ème année).
Remarque : cas du retour unitaire
Le système est à retour unitaire si la fonction de transfert de la boucle de retour vaut 1. On peut, dans ce
cas, comparer directement les valeurs d'entrée et de sortie (même grandeur physique).
E ε S
+ H
-
R
H p
Alors, la FTBO est égale à la fonction de transfert de la chaîne directe H et la FTBF vaut : .
1H p
Schémas-Blocs 3












