DEEL_008
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: brntmrchl
Type : Classeur 3.6
Page(s) : 10
Taille Size: 550.01 Ko KB
Mis en ligne Uploaded: 29/01/2020 - 03:23:16
Uploadeur Uploader: brntmrchl (Profil)
Téléchargements Downloads: 46
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2571450
Type : Classeur 3.6
Page(s) : 10
Taille Size: 550.01 Ko KB
Mis en ligne Uploaded: 29/01/2020 - 03:23:16
Uploadeur Uploader: brntmrchl (Profil)
Téléchargements Downloads: 46
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a2571450
Description
8 ROTATIE VAN EEN LICHAAM
ROTATIE VAN EEN LICHAAM
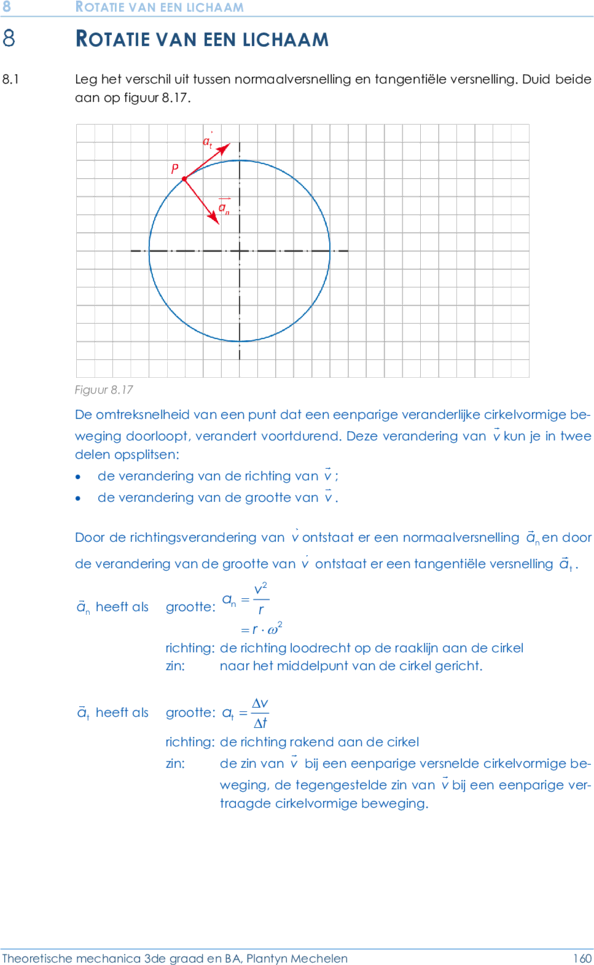
8.1 Leg het verschil uit tussen normaalversnelling en tangentiële versnelling. Duid beide
aan op figuur 8.17.
Figuur 8.17
De omtreksnelheid van een punt dat een eenparige veranderlijke cirkelvormige be-
weging doorloopt, verandert voortdurend. Deze verandering van v kun je in twee
delen opsplitsen:
de verandering van de richting van v ;
de verandering van de grootte van v .
Door de richtingsverandering van v ontstaat er een normaalversnelling an en door
de verandering van de grootte van v ontstaat er een tangentiële versnelling at .
v2
an
an heeft als grootte: r
r 2
richting: de richting loodrecht op de raaklijn aan de cirkel
zin: naar het middelpunt van de cirkel gericht.
v
at heeft als grootte: at
t
richting: de richting rakend aan de cirkel
zin: de zin van v bij een eenparige versnelde cirkelvormige be-
weging, de tegengestelde zin van v bij een eenparige ver-
traagde cirkelvormige beweging.
Theoretische mechanica 3de graad en BA, Plantyn Mechelen 160
8 ROTATIE VAN EEN LICHAAM
8.2 Waarom kun je de formule M J vergelijken met de tweede wet van Newton?
De grootheden van een rechtlijnige beweging kun je vergelijken met deze van een
cirkelvormige beweging.
Rechtlijnige Cirkelvormige
beweging beweging
Kracht – moment F M
Versnelling – hoekversnelling a
Massa - massatraagheidsmoment m J
Als je dit toepast op M J bekom je F m a , de tweede wet van Newton.
8.3 Wat is een massatraagheidsmoment?
Het massatraagheidsmoment is een maat voor de weerstand die een lichaam biedt
tegen elke roterende toestandsverandering.
Bij een rechtlijnige beweging is de massa de weerstand die een lichaam biedt tegen
een toestandsverandering. Je kunt het massatraagheidsmoment bij een ronddraai-
ende beweging dus vergelijken met de massa bij een rechtlijnige beweging.
8.4 Wanneer pas je de stelling van Steiner toe?
Als je een massatraagheidsmoment moet bepalen van een lichaam, ten opzichte
van een as die niet door het zwaartepuntvan het lichaam gaat dan pas je de stelling
van Steiner toe.
Ja Jx m ra2
8.5 Wat is de gyrostraal van een lichaam?
De gyrostraal of traagheidsstraal is de afstand van de rotatieas ten opzichte van een
punt met massa m, zodanig dat het massatraagheidsmoment van dat punt gelijk is
aan het massatraagheidsmoment van het lichaam dat door het punt werd vervan-
gen.
Theoretische mechanica 3de graad en BA, Plantyn Mechelen 161
8 ROTATIE VAN EEN LICHAAM
8.6 Een vliegwiel van een pers heeft een diameter van 1,1 m en een breedte van 0,4 m.
Bepaal het massatraagheidsmoment en de gyrostraal van het homogeen vliegwiel
( = 7 800 kg/m3).
Gegeven: D = 1,1 mm
b = 0,4 m
= 7 800 kg/m³
Gevraagd: J
k
Uitwerking
Volume van het vliegwiel
D2
V b
4
1,12
0,4 m2 m
4 Figuur 8.18 Pers
0,38 m3
Massa van het vliegwiel
mV
3 kg
0,38 7 800 m m3
2 965 kg
Massatraagheidsmoment van het vliegwiel
m R2
J
2
2 965 0,552
kg m2
2
448 kg m2
Gyrostraal
J
J k2 m k
m
448 kg m2
2 965 kg
0,389 m
Besluit: het massatraagheidsmoment van het vliegwiel is 448 kgm2 en de gy-
rostraal is 0,389 m.
Theoretische mechanica 3de graad en BA, Plantyn Mechelen 162
8 ROTATIE VAN EEN LICHAAM
8.7 Bereken het massatraagheidsmoment en de gyrostraal van de rotor van een asyn-
chrone motor. Veronderstel dat de massadichtheid van de rotor homogeen is en
6,9 kg/dm³ bedraagt.
Figuur 8.19 Asynchrone motor
Figuur 8.20 Afmetingen van de rotor
Gegeven: figuur 9.19
= 6 900 kg/m³
Gevraagd: J
k
Uitwerking
Cilinder 1
D2
V1 l
4
0,0422
0,2 m2 m
4
277 10-6 m3
m1 V1
3 kg
277 106 6 900 m m3
1,912 kg
m1 r 2
J1
2
1,912 0,0212
kg m2
2
0,422 10 3 kg m2
Theoretische mechanica 3de graad en BA, Plantyn Mechelen 163
8 ROTATIE VAN EEN LICHAAM
Cilinder 2
D2
V2 l
4
0,162
0,28 m2 m
4
5 630 10-6 m3
m2 V2
3 kg
5 630 106 6 900 m m3
38,8 kg
m2 r 2
J2
2
38,8 0,082
kg m2
2
124,3 103 kg m2
Cilinder 3
D2
V3 l
4
0,0422
0,1 m2 m
4
139 10-6 m3
m3 V3
3 kg
138,5 106 6 900 m m3
0,956 kg
m3 r 2
J3
2
0,956 0,0212
kg m2
2
0,211 103 kg m2
Massatraagheidsmoment
J J1 J2 J3
0,422 103 124,3 103 0,211 103 kg m2
125 103 kg m2
0,125 kg m2
Gyrostraal
J
J k2 m k
m
0,125 kg m2
1,912 38,8 0,956 kg
0,055 m
55 mm
Besluit: het massatraagheidsmoment van de rotor is 0,125 kgm2 en de gyrostraal
is 55 mm.
Theoretische mechanica 3de graad en BA, Plantyn Mechelen 164
8 ROTATIE VAN EEN LICHAAM
8.8 Bereken het massatraagheidsmoment en de gyrostraal van onderstaand stalen
vliegwiel. De massadichtheid is 7 800 kg/m³.
Figuur 8.21 Vliegwiel
Gegeven: figuur 9.20
= 7 800 kg/m3
Gevraagd: J, k
Uitwerking
Massatraagheidsmoment
Eenheid Wiel Uitsparin...
ROTATIE VAN EEN LICHAAM
8.1 Leg het verschil uit tussen normaalversnelling en tangentiële versnelling. Duid beide
aan op figuur 8.17.
Figuur 8.17
De omtreksnelheid van een punt dat een eenparige veranderlijke cirkelvormige be-
weging doorloopt, verandert voortdurend. Deze verandering van v kun je in twee
delen opsplitsen:
de verandering van de richting van v ;
de verandering van de grootte van v .
Door de richtingsverandering van v ontstaat er een normaalversnelling an en door
de verandering van de grootte van v ontstaat er een tangentiële versnelling at .
v2
an
an heeft als grootte: r
r 2
richting: de richting loodrecht op de raaklijn aan de cirkel
zin: naar het middelpunt van de cirkel gericht.
v
at heeft als grootte: at
t
richting: de richting rakend aan de cirkel
zin: de zin van v bij een eenparige versnelde cirkelvormige be-
weging, de tegengestelde zin van v bij een eenparige ver-
traagde cirkelvormige beweging.
Theoretische mechanica 3de graad en BA, Plantyn Mechelen 160
8 ROTATIE VAN EEN LICHAAM
8.2 Waarom kun je de formule M J vergelijken met de tweede wet van Newton?
De grootheden van een rechtlijnige beweging kun je vergelijken met deze van een
cirkelvormige beweging.
Rechtlijnige Cirkelvormige
beweging beweging
Kracht – moment F M
Versnelling – hoekversnelling a
Massa - massatraagheidsmoment m J
Als je dit toepast op M J bekom je F m a , de tweede wet van Newton.
8.3 Wat is een massatraagheidsmoment?
Het massatraagheidsmoment is een maat voor de weerstand die een lichaam biedt
tegen elke roterende toestandsverandering.
Bij een rechtlijnige beweging is de massa de weerstand die een lichaam biedt tegen
een toestandsverandering. Je kunt het massatraagheidsmoment bij een ronddraai-
ende beweging dus vergelijken met de massa bij een rechtlijnige beweging.
8.4 Wanneer pas je de stelling van Steiner toe?
Als je een massatraagheidsmoment moet bepalen van een lichaam, ten opzichte
van een as die niet door het zwaartepuntvan het lichaam gaat dan pas je de stelling
van Steiner toe.
Ja Jx m ra2
8.5 Wat is de gyrostraal van een lichaam?
De gyrostraal of traagheidsstraal is de afstand van de rotatieas ten opzichte van een
punt met massa m, zodanig dat het massatraagheidsmoment van dat punt gelijk is
aan het massatraagheidsmoment van het lichaam dat door het punt werd vervan-
gen.
Theoretische mechanica 3de graad en BA, Plantyn Mechelen 161
8 ROTATIE VAN EEN LICHAAM
8.6 Een vliegwiel van een pers heeft een diameter van 1,1 m en een breedte van 0,4 m.
Bepaal het massatraagheidsmoment en de gyrostraal van het homogeen vliegwiel
( = 7 800 kg/m3).
Gegeven: D = 1,1 mm
b = 0,4 m
= 7 800 kg/m³
Gevraagd: J
k
Uitwerking
Volume van het vliegwiel
D2
V b
4
1,12
0,4 m2 m
4 Figuur 8.18 Pers
0,38 m3
Massa van het vliegwiel
mV
3 kg
0,38 7 800 m m3
2 965 kg
Massatraagheidsmoment van het vliegwiel
m R2
J
2
2 965 0,552
kg m2
2
448 kg m2
Gyrostraal
J
J k2 m k
m
448 kg m2
2 965 kg
0,389 m
Besluit: het massatraagheidsmoment van het vliegwiel is 448 kgm2 en de gy-
rostraal is 0,389 m.
Theoretische mechanica 3de graad en BA, Plantyn Mechelen 162
8 ROTATIE VAN EEN LICHAAM
8.7 Bereken het massatraagheidsmoment en de gyrostraal van de rotor van een asyn-
chrone motor. Veronderstel dat de massadichtheid van de rotor homogeen is en
6,9 kg/dm³ bedraagt.
Figuur 8.19 Asynchrone motor
Figuur 8.20 Afmetingen van de rotor
Gegeven: figuur 9.19
= 6 900 kg/m³
Gevraagd: J
k
Uitwerking
Cilinder 1
D2
V1 l
4
0,0422
0,2 m2 m
4
277 10-6 m3
m1 V1
3 kg
277 106 6 900 m m3
1,912 kg
m1 r 2
J1
2
1,912 0,0212
kg m2
2
0,422 10 3 kg m2
Theoretische mechanica 3de graad en BA, Plantyn Mechelen 163
8 ROTATIE VAN EEN LICHAAM
Cilinder 2
D2
V2 l
4
0,162
0,28 m2 m
4
5 630 10-6 m3
m2 V2
3 kg
5 630 106 6 900 m m3
38,8 kg
m2 r 2
J2
2
38,8 0,082
kg m2
2
124,3 103 kg m2
Cilinder 3
D2
V3 l
4
0,0422
0,1 m2 m
4
139 10-6 m3
m3 V3
3 kg
138,5 106 6 900 m m3
0,956 kg
m3 r 2
J3
2
0,956 0,0212
kg m2
2
0,211 103 kg m2
Massatraagheidsmoment
J J1 J2 J3
0,422 103 124,3 103 0,211 103 kg m2
125 103 kg m2
0,125 kg m2
Gyrostraal
J
J k2 m k
m
0,125 kg m2
1,912 38,8 0,956 kg
0,055 m
55 mm
Besluit: het massatraagheidsmoment van de rotor is 0,125 kgm2 en de gyrostraal
is 55 mm.
Theoretische mechanica 3de graad en BA, Plantyn Mechelen 164
8 ROTATIE VAN EEN LICHAAM
8.8 Bereken het massatraagheidsmoment en de gyrostraal van onderstaand stalen
vliegwiel. De massadichtheid is 7 800 kg/m³.
Figuur 8.21 Vliegwiel
Gegeven: figuur 9.20
= 7 800 kg/m3
Gevraagd: J, k
Uitwerking
Massatraagheidsmoment
Eenheid Wiel Uitsparin...












