Je suis brésilien et je ne parle pas Français. Je m'excuse et si vous me le permettez, j'écrirai en Anglais dans ce post.
Also, sorry for my bad English too - I'm a Portugues native speaker.
I hope that this forum is active, in order to us talk about this issue.
I have a few calculators and sometimes I like to make some benchmark tests with them. Maybe the "Calculator Olympic Games", if you wish.
I use to figure tests that everyone can play.
But, this time, I tried something different and excluded the non-programable calculators.
My intentions were to analyze the native programming language and also a similar algorithm to them, in order to compare their performance (maybe it is interesting to post the results and the codes in another post).
Well, we all know that the Classpad does not have a native good programming environment when you have performance in mind (even more when you are dealing with numerical analys with a lot of loops). In this way, myself and all the other calculators agreed that we will allow CP330 to use CPLua in substitution of natural Casio Basic.
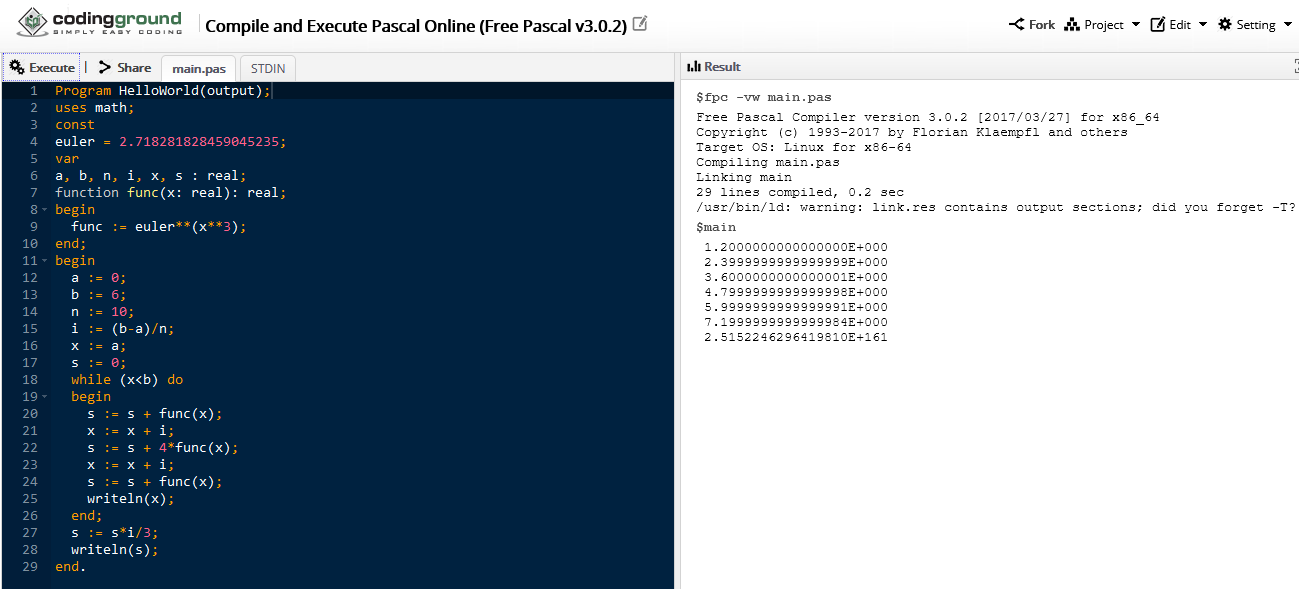
The benchmark used is to perform Simpson Rule as presented in this link for the Ti-81 (https://www.ticalc.org/pub/81/basic/math/simpson.81) PS: on line 5, the correct code is a capital i instead of one. The corrected instruction is : (B - A) / N -> I
The code was minor adjusted according the possible commands on each calculator.
So, they all have to perform the following definite integral:
e^(x^3), from 0 to 6, with n=1000
It was based on the test presented here: https://www.youtube.com/watch?v=DHRsvSTGiBc
The CPLua code used is:
- Code: Select all
--start
function y(x)
return math.exp(x^3)
end
n = 1000
a = 0 + 0.
b = 6 + 0.
i = (b-a)/n
x = a + 0.
s = 0.0
while ( x < b ) do
s = s+y(x)
x = x+i
s = 4*y(x)+s
x = x+i
s = s+y(x)
end
s = s*i/3
print(s)
Ok. All the calculators performed well and provided the same answer (obviously, with their respective performance time).
But CPLua in Classpad did not.
CPLua ignores when x = 6, when it should stop. It iterates one more time, as if the instruction were ( x <= b ) .
I tried everything that I figured that it could be and did not find anything. I tried CPLua 0.8 and 0.10a.
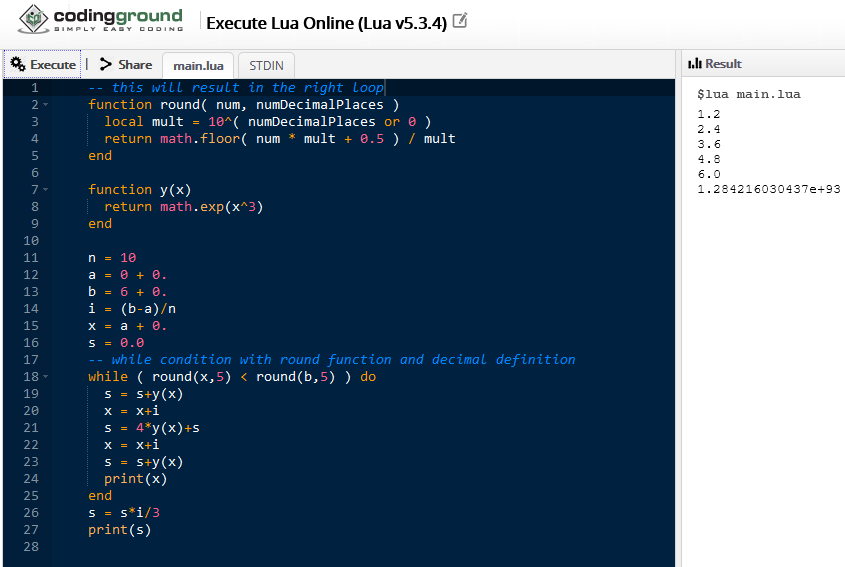
So, I changed the code, reduced the d to 10 and requested an x print before the while end. Just to investigate, the code became:
- Code: Select all
n = 10
a = 0 + 0.
b = 6 + 0.
i = (b-a)/n
x = a + 0.
s = 0.0
while ( x < b ) do
s = s+y(x)
x = x+i
s = 4*y(x)+s
x = x+i
s = s+y(x)
print(x)
end
s = s*i/3
print(s)
The output is:
1.2
2.4
3.6
4.8
6
7.2
2.51522462964201e+161
Done.
The 7.2 there is totaly wrong. It is not suposed to be there.
If I change b=5, so it works. If I change b to 6.000001 it works
But if I change b=6.00001 it does not work!!!!
Going a little bit further.
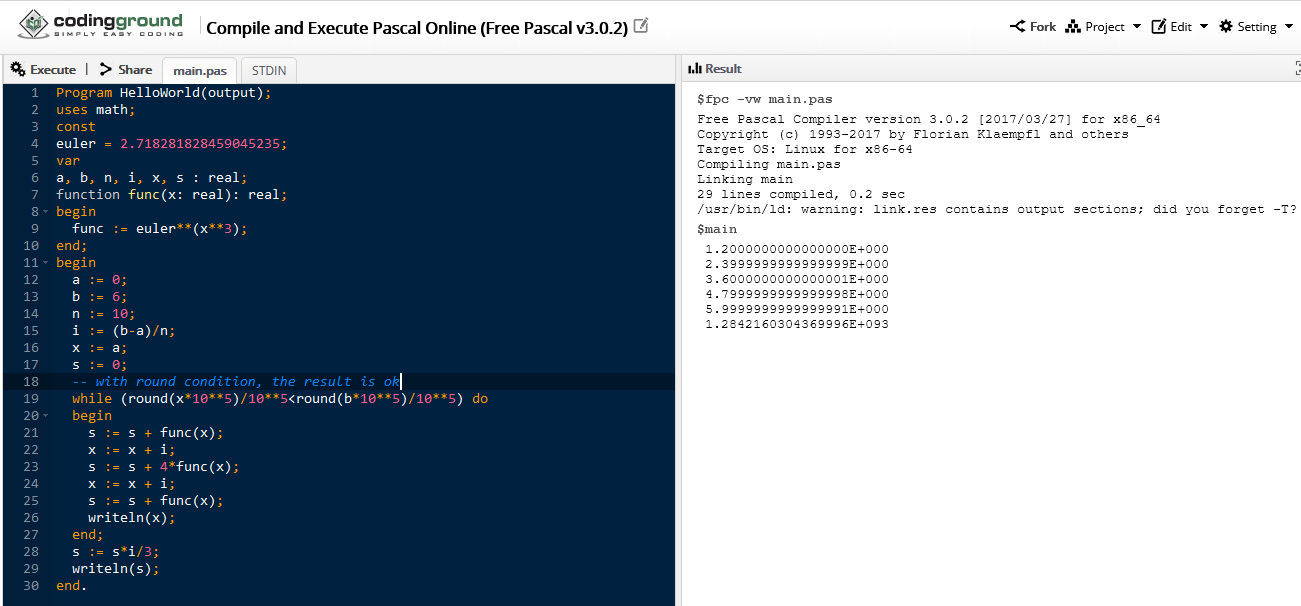
I implemented a function to round the x and the b value in the while condition. The function is (found somewhere, but I forgot to get the link):
- Code: Select all
function round( num, numDecimalPlaces )
local mult = 10^( numDecimalPlaces or 0 )
return math.floor( num * mult + 0.5 ) / mult
end
And the while condition became:
- Code: Select all
while ( round( x ) < round ( b ) ) do
The complete code is:
- Code: Select all
function round( num, numDecimalPlaces )
local mult = 10^( numDecimalPlaces or 0 )
return math.floor( num * mult + 0.5 ) / mult
end
function y(x)
return math.exp(x^3)
end
n = 10
a = 0 + 0.
b = 6 + 0.
i = (b-a)/n
x = a + 0.
s = 0.0
while ( round( x ) < round ( b ) ) do
s = s+y(x)
x = x+i
s = 4*y(x)+s
x = x+i
s = s+y(x)
print(x)
end
s = s*i/3
print(s)
It solved the problem but increased 25% in processing time
 .
. In another forum, I started the same discussion. Piu58 send some thoughts that I was think about also - maybe a base 10 to base 2 convertion could be the problem. The post is here https://community.casiocalc.org/topic/8069-cplua-what-is-wrong-with-this-while-loop/#entry63773
Taking this road, when a = 0, b = 6, n = 10, the value of i became i = 0.6
0.6 to base 2 is --> 0.6 (base10) = 0.10011001100110011001100110011... (base2) (it is recurring, as a repeating decimal, or in this way, a repeating binary? sorry for the bad english)
When we truncate the binary to the digits presented above and get back to base 10, we get:
0.10011001100110011001100110011 (base2) = 0.59999999962747097015 (base10)
For sure, anything that tries to represent 0.6 in binary and is truncated, will be lower than 0.6.
If we accumulate x with this i lower than 0.6 for 10 times, x will be something lower than 6.
buuuuuuut, when I asked to print (x), the CPLua presents x = 6 (in this way 10 times 0.6 - see the output presented in the begining of this post) and, in this way, it is representing x as 6 in base 10.
I am assuming that when I asked for x, CP330 and CPLua recognized x as 6, and give back to me a '6', so it printed x=6. I was expecting the same behavior in the while condition.
The algorithm in CP330 Casio Basic performs slowly (n = 100 it halts), but make the things right, and stops when x=6. Just in CPLua I got the problem.
So why did CPLua do not stop when x was 6? Does anybody knows why it is happening with CPLua?
Also, does anybody have any suggestion to how to solve it without the round() function in CPLua?