Episode 6:Dans l'épisode précédent, nous utilisions les suites
mathématiquement identiques:
u(n)=(10^-n)
v(n)=1+(10^-n)-1Et sur le tableau de valeurs affiché par une TI-82/83/84, nous constations une anomalie à partir du rang 13:
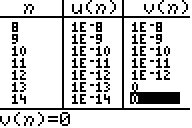
Bref,
1+(10^-13)-1=0 ...
Pour comprendre ce qu'il se passe, il faut penser les calculs, comme la machine.
Et donc, commençons à nous poser la question: pour la machine, c'est quoi un nombre?
Vous croyiez que votre calculatrice travaillait sur l'ensemble des réels?
Et bien non, même si elle fait tout pour vous en donner l'illusion...
En mémoire la calculatrice code toute valeur sur seulement 13 chiffres significatifs signés, munis d'une puissance de 10 signée sur 2 chiffres significatifs, bref des nombres décimaux.
Cela donne la forme suivante:
[tableborder=1]
| [table border=0] |
| [table border=1] |
| +/- | _ |
[/table]
, | [tableborder=1] | | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ | _ |
[/table]
| *10^ | [tableborder=1] | | +/- | _ | _ |
[/table][/table]
[/table]
Cela ne laisse qu'environ 2*10^13*2*10^2=4*10^15 nombres décimaux différents (4 millions de milliards)
Comme il existe une infinité de nombre décimaux, qui de plus ne sont qu'un sous-ensemble des réels, on en est très loin...
Il est absolument impossible pour la calculatrice d'écrire/mémoriser quoi que ce soit en dehors de ce tableau.
Par exemple 123,45 est codé en mémoire comme:
[tableborder=1]
| [table border=0] |
| [table border=1] |
| + | 1 |
[/table]
, | [tableborder=1] | | 2 | 3 | 4 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
[/table]
| *10^ | [tableborder=1] | | + | 0 | 2 |
[/table][/table]
[/table]
Bref, la calculatrice manipule des notations scientifiques (vu en Troisième).
Et pour faire des additions/soustractions en notation scientifique, je vous rappelle qu'il faut convertir sous la même puissance de 10...
Alors essayez de faire le calcul
1+(10^-13)-1 en n'inscrivant que des valeurs DANS le tableau vierge ci-dessus.
















 )
)





