moteur a courant continu
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: Eazye
Type : Classeur 3.6
Page(s) : 4
Taille Size: 166.30 Ko KB
Mis en ligne Uploaded: 04/05/2015 - 11:04:32
Uploadeur Uploader: Eazye (Profil)
Téléchargements Downloads: 621
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a209153
Type : Classeur 3.6
Page(s) : 4
Taille Size: 166.30 Ko KB
Mis en ligne Uploaded: 04/05/2015 - 11:04:32
Uploadeur Uploader: Eazye (Profil)
Téléchargements Downloads: 621
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a209153
Description
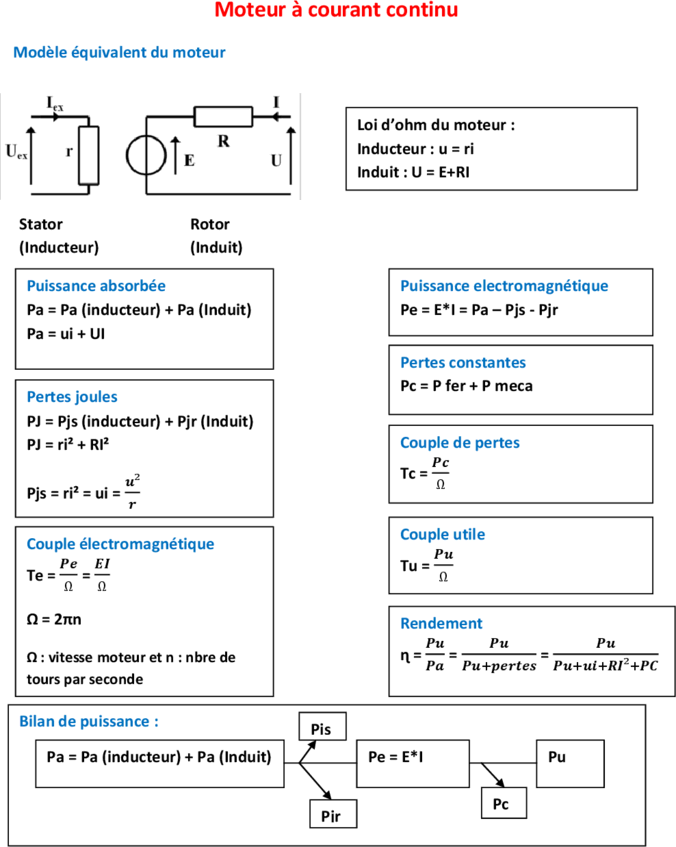
Moteur à courant continu
Modèle équivalent du moteur
Loi d’ohm du moteur :
Inducteur : u = ri
Induit : U = E+RI
Stator Rotor
(Inducteur) (Induit)
Puissance absorbée Puissance electromagnétique
Pa = Pa (inducteur) + Pa (Induit) Pe = E*I = Pa – Pjs - Pjr
Pa = ui + UI
Pertes constantes
Pc = P fer + P meca
Pertes joules
PJ = Pjs (inducteur) + Pjr (Induit)
PJ = ri² + RI² Couple de pertes
Tc =
Pjs = ri² = ui =
Couple utile
Couple électromagnétique
Tu =
Te = =
Ω = 2πn Rendement
Ω : vitesse moteur et n : nbre de ɳ= = =
tours par seconde
Bilan de puissance : Pjs
Pa = Pa (inducteur) + Pa (Induit) Pe = E*I Pu
Pc
Pjr
Moteur au démarrage
On a Ud = Ed + RID or Ed = k nd ( la fem est
proportionnelle à la vitesse au démarrage nd = 0 )
Alors on a Ed = 0 et Ud = RId et Id =
Moteur à excitation indépendante
Loi d’ohm du moteur :
Inducteur : u = ri
Induit : U = E+RI
Moteur à excitation en série
Loi d’ohm du moteur : U’ = E ( R+r ) I
Moteur à excitation Shunt ou en parallèle
Pjs
Pa = U I’ Pe = E*I Pu = Tu Ω
Pc
Pjr
Lien vitesse et FEM
E = * *o*Ω P : paire de pole a : nbre de voie d’enroulement
N : nbre de conducteur actif o : flux sous un pole Ω : vitesse de rotation
A une vitesse n1 : E1 = kn1 =
A une vitesse n2 : E2 = kn2
Vitesse : E = U-RI U – RI = Pa*N*n*o or =1
E= *N*n*o
n=
Ne jamais débrancher le stator quand le moteur est en rotation
Lien entre le couple électromagnétique et le courant
Pe = EI EI = Te Ω et Te =
Pe = Te Ω
A un fonctionnement 1 : Te1 = kI1 =
A un fonctionnement 2 : Te2 = KI2
Lien couple et vitesse
Te = kI or n= I= Te = k ( ) Te = – = +
Expression de la forme y = ax + b avec a = et b =
Représentation graphique
Couple pertes
Te – Tp = Tu Pu = Tu Ω P pertes = Tp Ω
Modèle équivalent du moteur
Loi d’ohm du moteur :
Inducteur : u = ri
Induit : U = E+RI
Stator Rotor
(Inducteur) (Induit)
Puissance absorbée Puissance electromagnétique
Pa = Pa (inducteur) + Pa (Induit) Pe = E*I = Pa – Pjs - Pjr
Pa = ui + UI
Pertes constantes
Pc = P fer + P meca
Pertes joules
PJ = Pjs (inducteur) + Pjr (Induit)
PJ = ri² + RI² Couple de pertes
Tc =
Pjs = ri² = ui =
Couple utile
Couple électromagnétique
Tu =
Te = =
Ω = 2πn Rendement
Ω : vitesse moteur et n : nbre de ɳ= = =
tours par seconde
Bilan de puissance : Pjs
Pa = Pa (inducteur) + Pa (Induit) Pe = E*I Pu
Pc
Pjr
Moteur au démarrage
On a Ud = Ed + RID or Ed = k nd ( la fem est
proportionnelle à la vitesse au démarrage nd = 0 )
Alors on a Ed = 0 et Ud = RId et Id =
Moteur à excitation indépendante
Loi d’ohm du moteur :
Inducteur : u = ri
Induit : U = E+RI
Moteur à excitation en série
Loi d’ohm du moteur : U’ = E ( R+r ) I
Moteur à excitation Shunt ou en parallèle
Pjs
Pa = U I’ Pe = E*I Pu = Tu Ω
Pc
Pjr
Lien vitesse et FEM
E = * *o*Ω P : paire de pole a : nbre de voie d’enroulement
N : nbre de conducteur actif o : flux sous un pole Ω : vitesse de rotation
A une vitesse n1 : E1 = kn1 =
A une vitesse n2 : E2 = kn2
Vitesse : E = U-RI U – RI = Pa*N*n*o or =1
E= *N*n*o
n=
Ne jamais débrancher le stator quand le moteur est en rotation
Lien entre le couple électromagnétique et le courant
Pe = EI EI = Te Ω et Te =
Pe = Te Ω
A un fonctionnement 1 : Te1 = kI1 =
A un fonctionnement 2 : Te2 = KI2
Lien couple et vitesse
Te = kI or n= I= Te = k ( ) Te = – = +
Expression de la forme y = ax + b avec a = et b =
Représentation graphique
Couple pertes
Te – Tp = Tu Pu = Tu Ω P pertes = Tp Ω












