décrire le mouvement d'un corps meca 1
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: omar1998
Type : Classeur 3.6
Page(s) : 12
Taille Size: 1.12 Mo MB
Mis en ligne Uploaded: 10/03/2019 - 17:51:24
Uploadeur Uploader: omar1998 (Profil)
Téléchargements Downloads: 30
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a1968714
Type : Classeur 3.6
Page(s) : 12
Taille Size: 1.12 Mo MB
Mis en ligne Uploaded: 10/03/2019 - 17:51:24
Uploadeur Uploader: omar1998 (Profil)
Téléchargements Downloads: 30
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a1968714
Description
Sciences Physiques - Chimie MPSI
Partie 4 : Mécanique 1 - Ch.1 : Cinématique du point (et du solide)
Ch.1 Cinématique du point (et du solide)
(ie) Comment décrire le mouvement d'un corps ?
L'objectif de la mécanique est d'étudier le mouvement d'un corps. La cinématique a pour
objet la description du mouvement d'un corps sans chercher à en déterminer les causes (c'est à dire
les forces qui s'appliquent sur ce corps).
Pour décrire ce mouvement, il faut réaliser des mesures grâce à des observateurs (personnes
physiques ou appareils de mesures). Ces observateurs mesurent des positions et des temps dans le
système international d'unités.
Les positions sont mesurées à l'aide d'un système de coordonnées, appelé repère. Ce repère
est associé à un solide (corps indéformable).
Le temps est mesuré à l'aide d'un appareil de mesure du temps, appelé horloge.
Ces observateurs doivent donc choisir un repère et une horloge. Ce couple repère-horloge
est appelé le référentiel de l'observateur.
• Caractère relatif du mouvement et choix du référentiel
Selon l'observateur qui réalise l'étude, le mouvement d'un corps va être différent. C'est le caractère
relatif du mouvement.
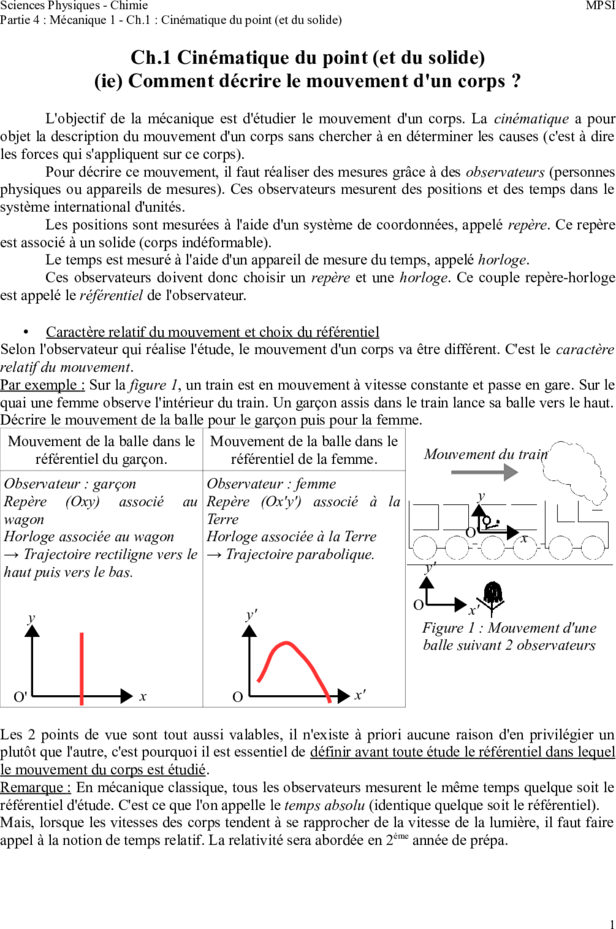
Par exemple : Sur la figure 1, un train est en mouvement à vitesse constante et passe en gare. Sur le
quai une femme observe l'intérieur du train. Un garçon assis dans le train lance sa balle vers le haut.
Décrire le mouvement de la balle pour le garçon puis pour la femme.
Mouvement de la balle dans le Mouvement de la balle dans le
référentiel du garçon. référentiel de la femme. Mouvement du train
Observateur : garçon Observateur : femme
Repère (Oxy) associé au Repère (Ox'y') associé à la y
wagon Terre
Horloge associée au wagon Horloge associée à la Terre O' x
→ Trajectoire rectiligne vers le → Trajectoire parabolique.
haut puis vers le bas. y'
O x'
y y'
Figure 1 : Mouvement d'une
balle suivant 2 observateurs
O' x O x'
Les 2 points de vue sont tout aussi valables, il n'existe à priori aucune raison d'en privilégier un
plutôt que l'autre, c'est pourquoi il est essentiel de définir avant toute étude le référentiel dans lequel
le mouvement du corps est étudié.
Remarque : En mécanique classique, tous les observateurs mesurent le même temps quelque soit le
référentiel d'étude. C'est ce que l'on appelle le temps absolu (identique quelque soit le référentiel).
Mais, lorsque les vitesses des corps tendent à se rapprocher de la vitesse de la lumière, il faut faire
appel à la notion de temps relatif. La relativité sera abordée en 2éme année de prépa.
1
Sciences Physiques - Chimie MPSI
Partie 4 : Mécanique 1 - Ch.1 : Cinématique du point (et du solide)
Le repère lié à un solide est défini par un point fixe du solide, appelé l'origine du repère et 3
vecteurs ( ⃗u1 ,⃗
u2 , ⃗
u 3) dans 3 directions de l'espace, appelée la base du repère. En pratique, on
choisit toujours une base :
• Orthonormée :
◦ Normée : ∥⃗ u 1∥=∥⃗
u 2∥=∥⃗
u 3∥=1 : les vecteurs ⃗ u1 , ⃗
u2 , ⃗
u 3 sont dits unitaires.
◦ Orthogonale : les vecteurs sont orthogonaux entre eux.
• Directe : règle de la main droite : ⃗ u 1 ⇔ pouce , ⃗
u 2 ⇔ index , ⃗ u 3 ⇔ majeur .
I. Grandeurs vectorielles
En mécanique, on va définir position, vitesse et accélération d'un corps à l'aide de 3
coordonnées, ce qui définit un vecteur.
Rappelons quelques propriétés d'un vecteur ⃗ u x ,⃗
A dans une base orthonormée ( ⃗ uy ,⃗
uz )
I.1. Produit scalaire
• Le produit scalaire de 2 vecteurs ⃗A et ⃗ B se définit par :
⃗ B=∥⃗
A .⃗ A∥∥⃗B∥cos ( ⃗
A ,⃗
B) avec : ( A , B) : angle entre les vecteurs ⃗
⃗ ⃗ A et ⃗
B (A dessiner)
• Le produit scalaire est symétrique : ⃗ A .⃗
B=⃗ B.⃗A
• Le produit scalaire est distributif : ( ⃗
A+⃗ B). ⃗
C=⃗ A. ⃗
C+⃗
B.⃗
C
• Remarques :
◦ Si ⃗ A et ⃗
B sont colinéaires : ⃗ B=∥⃗
A .⃗ A∥∥⃗B∥
⃗ ⃗
◦ Si A et B sont orthogonaux : A . B=0⃗ ⃗
I.2. Projection d'un vecteur
A
• Soit un vecteur ⃗ A , on nomme projection de ⃗ A
u x la quantité :
sur le vecteur unitaire ⃗ q
⃗ u x =∥⃗
A .⃗ A∥cos (θ) avec θ=(⃗ u x ) (figure 2)
A ,⃗ O Ax
ux
⃗
• La coordonnée Ax du vecteur ⃗ A est alors définie Figure 2 : projection de A sur⃗
ux
comme le résultat de cette projection de ⃗ A sur ⃗ u x : A x =⃗ u x (figure 2)
A.⃗
• Les coordonnées ( A x , A y , Az ) du vecteur A sont alors naturellement définies comme les
⃗
A sur les 3 vecteurs u⃗x , ⃗
projections de ⃗ u y ,⃗
u z de la base.
Le vecteur ⃗ A s'écrit : ⃗
A= A x ⃗ u x +A y ⃗
uy+ A z ⃗
uz
• On peut alors montrer que : ⃗ A .⃗
B= Ax B x +A y B y + Az B z
⃗
A .⃗
B=( A x ⃗
u x +A y ⃗
u y +A z ⃗ u z ).( B x ⃗
u x +B y ⃗u y +B z ⃗
uz)
⃗ ⃗
Donc : A . B= Ax . B x ⃗ ux . ⃗
u x +A y B x ⃗ uy⃗ u y +...
2
Or : ⃗ u x =∥⃗
u x .⃗ u x∥ =1 et ⃗
uy.⃗
u x =⃗ u x =0 donc on retrouve : ⃗
uz .⃗ A .⃗
B= Ax B x +A y B y + Az B z
2
Sciences Physiques - Chimie MPSI
Partie 4 : Mécanique 1 - Ch.1 : Cinématique du point (et du solide)
II. Systèmes de coordonnées et vecteur-position
Soit O l'origine du repère, la position d'un point M à un instant t est définie par le vecteur-position :
⃗r (t)=⃗ OM (t) . Il faut alors décrire ce vecteur à l'aide de coordonnées.
II.1. Coordonnées cartésiennes
Les coordonnées cartésiennes sont définies par le découpage de l'espace
en carré de taille donnée (figure 3). Dans un tel espace, il est possible de
définir la position d'un point M quelconque de l'espace.
Les coordonnées cartésiennes du point M sont notées : (x , y , z)
Figure 3 : Découpage de H
l'espace en carré
En 3D, on définit le rep
Partie 4 : Mécanique 1 - Ch.1 : Cinématique du point (et du solide)
Ch.1 Cinématique du point (et du solide)
(ie) Comment décrire le mouvement d'un corps ?
L'objectif de la mécanique est d'étudier le mouvement d'un corps. La cinématique a pour
objet la description du mouvement d'un corps sans chercher à en déterminer les causes (c'est à dire
les forces qui s'appliquent sur ce corps).
Pour décrire ce mouvement, il faut réaliser des mesures grâce à des observateurs (personnes
physiques ou appareils de mesures). Ces observateurs mesurent des positions et des temps dans le
système international d'unités.
Les positions sont mesurées à l'aide d'un système de coordonnées, appelé repère. Ce repère
est associé à un solide (corps indéformable).
Le temps est mesuré à l'aide d'un appareil de mesure du temps, appelé horloge.
Ces observateurs doivent donc choisir un repère et une horloge. Ce couple repère-horloge
est appelé le référentiel de l'observateur.
• Caractère relatif du mouvement et choix du référentiel
Selon l'observateur qui réalise l'étude, le mouvement d'un corps va être différent. C'est le caractère
relatif du mouvement.
Par exemple : Sur la figure 1, un train est en mouvement à vitesse constante et passe en gare. Sur le
quai une femme observe l'intérieur du train. Un garçon assis dans le train lance sa balle vers le haut.
Décrire le mouvement de la balle pour le garçon puis pour la femme.
Mouvement de la balle dans le Mouvement de la balle dans le
référentiel du garçon. référentiel de la femme. Mouvement du train
Observateur : garçon Observateur : femme
Repère (Oxy) associé au Repère (Ox'y') associé à la y
wagon Terre
Horloge associée au wagon Horloge associée à la Terre O' x
→ Trajectoire rectiligne vers le → Trajectoire parabolique.
haut puis vers le bas. y'
O x'
y y'
Figure 1 : Mouvement d'une
balle suivant 2 observateurs
O' x O x'
Les 2 points de vue sont tout aussi valables, il n'existe à priori aucune raison d'en privilégier un
plutôt que l'autre, c'est pourquoi il est essentiel de définir avant toute étude le référentiel dans lequel
le mouvement du corps est étudié.
Remarque : En mécanique classique, tous les observateurs mesurent le même temps quelque soit le
référentiel d'étude. C'est ce que l'on appelle le temps absolu (identique quelque soit le référentiel).
Mais, lorsque les vitesses des corps tendent à se rapprocher de la vitesse de la lumière, il faut faire
appel à la notion de temps relatif. La relativité sera abordée en 2éme année de prépa.
1
Sciences Physiques - Chimie MPSI
Partie 4 : Mécanique 1 - Ch.1 : Cinématique du point (et du solide)
Le repère lié à un solide est défini par un point fixe du solide, appelé l'origine du repère et 3
vecteurs ( ⃗u1 ,⃗
u2 , ⃗
u 3) dans 3 directions de l'espace, appelée la base du repère. En pratique, on
choisit toujours une base :
• Orthonormée :
◦ Normée : ∥⃗ u 1∥=∥⃗
u 2∥=∥⃗
u 3∥=1 : les vecteurs ⃗ u1 , ⃗
u2 , ⃗
u 3 sont dits unitaires.
◦ Orthogonale : les vecteurs sont orthogonaux entre eux.
• Directe : règle de la main droite : ⃗ u 1 ⇔ pouce , ⃗
u 2 ⇔ index , ⃗ u 3 ⇔ majeur .
I. Grandeurs vectorielles
En mécanique, on va définir position, vitesse et accélération d'un corps à l'aide de 3
coordonnées, ce qui définit un vecteur.
Rappelons quelques propriétés d'un vecteur ⃗ u x ,⃗
A dans une base orthonormée ( ⃗ uy ,⃗
uz )
I.1. Produit scalaire
• Le produit scalaire de 2 vecteurs ⃗A et ⃗ B se définit par :
⃗ B=∥⃗
A .⃗ A∥∥⃗B∥cos ( ⃗
A ,⃗
B) avec : ( A , B) : angle entre les vecteurs ⃗
⃗ ⃗ A et ⃗
B (A dessiner)
• Le produit scalaire est symétrique : ⃗ A .⃗
B=⃗ B.⃗A
• Le produit scalaire est distributif : ( ⃗
A+⃗ B). ⃗
C=⃗ A. ⃗
C+⃗
B.⃗
C
• Remarques :
◦ Si ⃗ A et ⃗
B sont colinéaires : ⃗ B=∥⃗
A .⃗ A∥∥⃗B∥
⃗ ⃗
◦ Si A et B sont orthogonaux : A . B=0⃗ ⃗
I.2. Projection d'un vecteur
A
• Soit un vecteur ⃗ A , on nomme projection de ⃗ A
u x la quantité :
sur le vecteur unitaire ⃗ q
⃗ u x =∥⃗
A .⃗ A∥cos (θ) avec θ=(⃗ u x ) (figure 2)
A ,⃗ O Ax
ux
⃗
• La coordonnée Ax du vecteur ⃗ A est alors définie Figure 2 : projection de A sur⃗
ux
comme le résultat de cette projection de ⃗ A sur ⃗ u x : A x =⃗ u x (figure 2)
A.⃗
• Les coordonnées ( A x , A y , Az ) du vecteur A sont alors naturellement définies comme les
⃗
A sur les 3 vecteurs u⃗x , ⃗
projections de ⃗ u y ,⃗
u z de la base.
Le vecteur ⃗ A s'écrit : ⃗
A= A x ⃗ u x +A y ⃗
uy+ A z ⃗
uz
• On peut alors montrer que : ⃗ A .⃗
B= Ax B x +A y B y + Az B z
⃗
A .⃗
B=( A x ⃗
u x +A y ⃗
u y +A z ⃗ u z ).( B x ⃗
u x +B y ⃗u y +B z ⃗
uz)
⃗ ⃗
Donc : A . B= Ax . B x ⃗ ux . ⃗
u x +A y B x ⃗ uy⃗ u y +...
2
Or : ⃗ u x =∥⃗
u x .⃗ u x∥ =1 et ⃗
uy.⃗
u x =⃗ u x =0 donc on retrouve : ⃗
uz .⃗ A .⃗
B= Ax B x +A y B y + Az B z
2
Sciences Physiques - Chimie MPSI
Partie 4 : Mécanique 1 - Ch.1 : Cinématique du point (et du solide)
II. Systèmes de coordonnées et vecteur-position
Soit O l'origine du repère, la position d'un point M à un instant t est définie par le vecteur-position :
⃗r (t)=⃗ OM (t) . Il faut alors décrire ce vecteur à l'aide de coordonnées.
II.1. Coordonnées cartésiennes
Les coordonnées cartésiennes sont définies par le découpage de l'espace
en carré de taille donnée (figure 3). Dans un tel espace, il est possible de
définir la position d'un point M quelconque de l'espace.
Les coordonnées cartésiennes du point M sont notées : (x , y , z)
Figure 3 : Découpage de H
l'espace en carré
En 3D, on définit le rep












