Développements en séries entières usuels
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: styllerz
Type : Classeur 3.6
Page(s) : 2
Taille Size: 85.81 Ko KB
Mis en ligne Uploaded: 20/04/2015 - 12:23:34
Mis à jour Updated: 20/04/2015 - 12:24:12
Uploadeur Uploader: styllerz (Profil)
Téléchargements Downloads: 290
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a196506
Type : Classeur 3.6
Page(s) : 2
Taille Size: 85.81 Ko KB
Mis en ligne Uploaded: 20/04/2015 - 12:23:34
Mis à jour Updated: 20/04/2015 - 12:24:12
Uploadeur Uploader: styllerz (Profil)
Téléchargements Downloads: 290
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a196506
Description
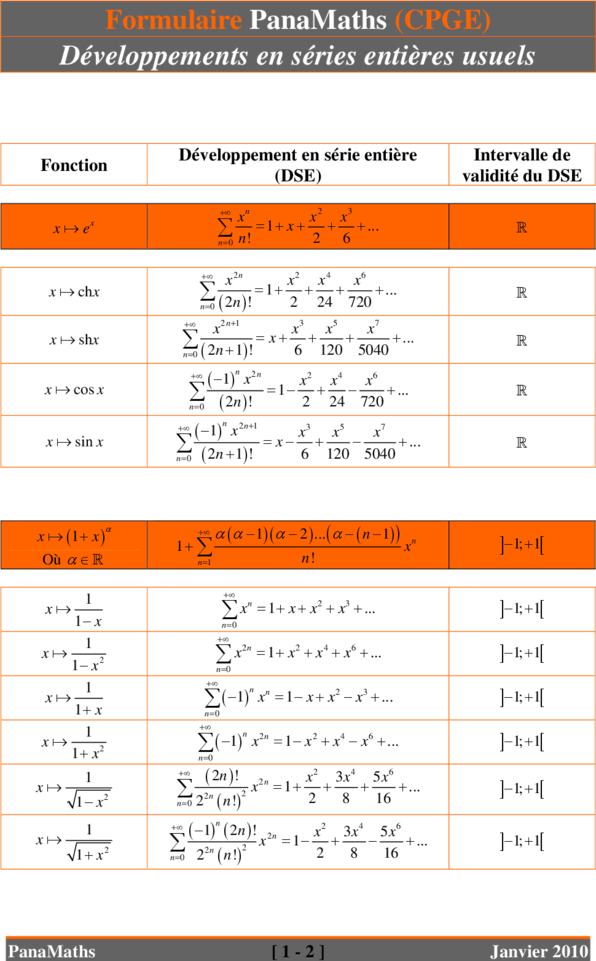
Formulaire PanaMaths (CPGE)
Développements en séries entières usuels
Développement en série entière Intervalle de
Fonction
(DSE) validité du DSE
+∞
xn x 2 x3
x6e x
∑
n=0 n !
= 1 + x + + + ...
2 6
+∞
x2n x2 x4 x6
x 6 chx ∑
n = 0 ( 2n ) !
= 1 + + +
2 24 720
+ ...
+∞
x 2 n +1 x3 x5 x7
x 6 shx ∑
n = 0 ( 2 n + 1) !
= x + + +
6 120 5040
+ ...
( −1) x 2 n = 1 − x 2 + x 4 − x 6 + ...
n
+∞
x 6 cos x ∑n =0 ( 2n ) ! 2 24 720
( −1) x 2 n+1 = x − x3 + x5 − x 7 + ...
n
+∞
x 6 sin x ∑
n = 0 ( 2n + 1) ! 6 120 5040
x 6 (1 + x )
α +∞ α (α − 1)(α − 2 ) ... (α − ( n − 1) )
1+ ∑ xn ]−1; +1[
Où α ∈ n =1 n!
+∞
∑x
1
x6 n
= 1 + x + x 2 + x3 + ... ]−1; +1[
1− x n =0
+∞
∑x
1
x6 2n
= 1 + x 2 + x 4 + x 6 + ... ]−1; +1[
1 − x2 n =0
+∞
∑ ( −1)
1
x n = 1 − x + x 2 − x3 + ... ]−1; +1[
n
x6
1+ x n =0
+∞
∑ ( −1)
1
x 2 n = 1 − x 2 + x 4 − x 6 + ... ]−1; +1[
n
x6
1 + x2 n =0
1 +∞
( 2n )! x 2 n = 1 + x 2 + 3x 4 + 5 x 6 + ...
x6 ∑
n = 0 2 ( n !)
2 ]−1; +1[
1 − x2
2n
2 8 16
( −1) ( 2n )! x 2 n = 1 − x 2 + 3x 4 − 5 x 6 + ...
n
+∞
1
x6 ∑ ]−1; +1[
1 + x2 n = 0 2 ( n !)
2n 2
2 8 16
PanaMaths [1-2] Janvier 2010
+∞
xn x 2 x3 x 4
x 6 ln (1 − x ) −∑ = − x − − − − ... ]−1; +1[
n =1 n 2 3 4
+∞
x 2 n +1 x3 x5 x 7
x 6 arg tanh x ∑ = 1 + + + + ... ]−1; +1[
n = 0 2n + 1 3 5 7
( −1)
n +1
+∞
xn x 2 x3 x 4
x 6 ln (1 + x ) ∑ = x− + − + ... ]−1; +1[
n =1 n 2 3 4
+∞
x 2 n +1 x3 x5 x 7
x 6 arctan x ∑ ( −1)
n
= x − + − + ... ]−1; +1[
n =0 2n + 1 3 5 7
+∞
( 2n )! x 2 n+1 = x + x3 + 3x5 + 5 x 7 + ...
x 6 arcsin x ∑2 ]−1; +1[
( n !) 2n + 1
2n 2
n=0 6 40 112
π +∞ ( 2n ) ! x 2 n +1 π x3 3 x5
x 6 arccos x −∑ = −x− − − ... ]−1; +1[
2 n =0 22 n ( n !)2 2n + 1 2 6 40
( −1) ( 2n )! x 2 n+1 = x − x3 + 3x5 − 5 x 7 + ...
n
+∞
x 6 arg sinh x ∑ ]−1; +1[
n = 0 2 ( n !) 2n + 1
2n 2
6 40 112
PanaMaths [2-2] Janvier 2010
Développements en séries entières usuels
Développement en série entière Intervalle de
Fonction
(DSE) validité du DSE
+∞
xn x 2 x3
x6e x
∑
n=0 n !
= 1 + x + + + ...
2 6
+∞
x2n x2 x4 x6
x 6 chx ∑
n = 0 ( 2n ) !
= 1 + + +
2 24 720
+ ...
+∞
x 2 n +1 x3 x5 x7
x 6 shx ∑
n = 0 ( 2 n + 1) !
= x + + +
6 120 5040
+ ...
( −1) x 2 n = 1 − x 2 + x 4 − x 6 + ...
n
+∞
x 6 cos x ∑n =0 ( 2n ) ! 2 24 720
( −1) x 2 n+1 = x − x3 + x5 − x 7 + ...
n
+∞
x 6 sin x ∑
n = 0 ( 2n + 1) ! 6 120 5040
x 6 (1 + x )
α +∞ α (α − 1)(α − 2 ) ... (α − ( n − 1) )
1+ ∑ xn ]−1; +1[
Où α ∈ n =1 n!
+∞
∑x
1
x6 n
= 1 + x + x 2 + x3 + ... ]−1; +1[
1− x n =0
+∞
∑x
1
x6 2n
= 1 + x 2 + x 4 + x 6 + ... ]−1; +1[
1 − x2 n =0
+∞
∑ ( −1)
1
x n = 1 − x + x 2 − x3 + ... ]−1; +1[
n
x6
1+ x n =0
+∞
∑ ( −1)
1
x 2 n = 1 − x 2 + x 4 − x 6 + ... ]−1; +1[
n
x6
1 + x2 n =0
1 +∞
( 2n )! x 2 n = 1 + x 2 + 3x 4 + 5 x 6 + ...
x6 ∑
n = 0 2 ( n !)
2 ]−1; +1[
1 − x2
2n
2 8 16
( −1) ( 2n )! x 2 n = 1 − x 2 + 3x 4 − 5 x 6 + ...
n
+∞
1
x6 ∑ ]−1; +1[
1 + x2 n = 0 2 ( n !)
2n 2
2 8 16
PanaMaths [1-2] Janvier 2010
+∞
xn x 2 x3 x 4
x 6 ln (1 − x ) −∑ = − x − − − − ... ]−1; +1[
n =1 n 2 3 4
+∞
x 2 n +1 x3 x5 x 7
x 6 arg tanh x ∑ = 1 + + + + ... ]−1; +1[
n = 0 2n + 1 3 5 7
( −1)
n +1
+∞
xn x 2 x3 x 4
x 6 ln (1 + x ) ∑ = x− + − + ... ]−1; +1[
n =1 n 2 3 4
+∞
x 2 n +1 x3 x5 x 7
x 6 arctan x ∑ ( −1)
n
= x − + − + ... ]−1; +1[
n =0 2n + 1 3 5 7
+∞
( 2n )! x 2 n+1 = x + x3 + 3x5 + 5 x 7 + ...
x 6 arcsin x ∑2 ]−1; +1[
( n !) 2n + 1
2n 2
n=0 6 40 112
π +∞ ( 2n ) ! x 2 n +1 π x3 3 x5
x 6 arccos x −∑ = −x− − − ... ]−1; +1[
2 n =0 22 n ( n !)2 2n + 1 2 6 40
( −1) ( 2n )! x 2 n+1 = x − x3 + 3x5 − 5 x 7 + ...
n
+∞
x 6 arg sinh x ∑ ]−1; +1[
n = 0 2 ( n !) 2n + 1
2n 2
6 40 112
PanaMaths [2-2] Janvier 2010












