Méthodes
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: solerem
Type : Classeur 3.6
Page(s) : 6
Taille Size: 182.35 Ko KB
Mis en ligne Uploaded: 03/11/2018 - 14:40:09
Uploadeur Uploader: solerem (Profil)
Téléchargements Downloads: 30
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a1770240
Type : Classeur 3.6
Page(s) : 6
Taille Size: 182.35 Ko KB
Mis en ligne Uploaded: 03/11/2018 - 14:40:09
Uploadeur Uploader: solerem (Profil)
Téléchargements Downloads: 30
Visibilité Visibility: Archive publique
Shortlink : http://ti-pla.net/a1770240
Description
Chapitre 4 Terminale S
Les matrices Déterminer par le calcul une matrice inverse Mathématiques
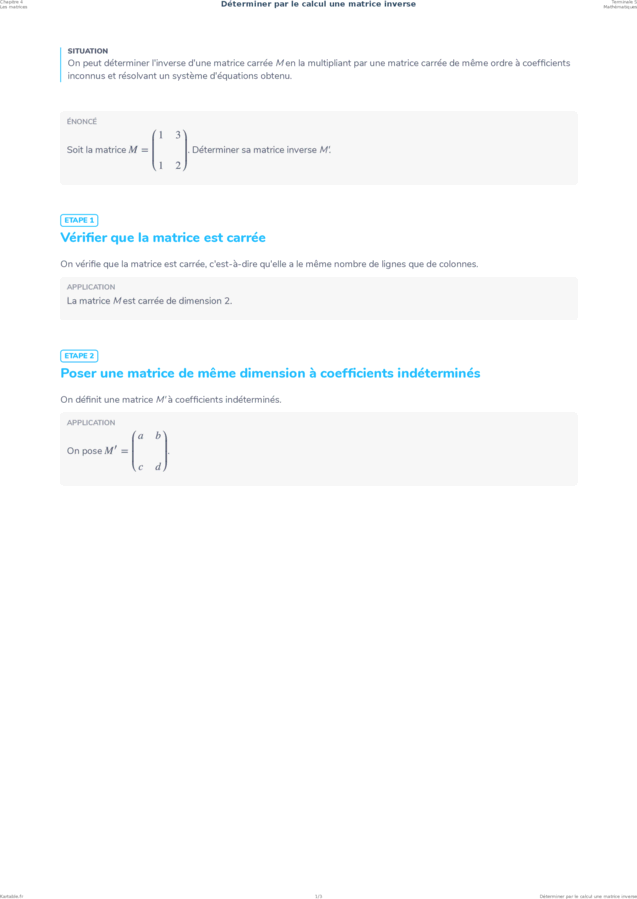
SITUATION
On peut déterminer l'inverse d'une matrice carrée M en la multipliant par une matrice carrée de même ordre à coef cients
inconnus et résolvant un système d'équations obtenu.
1 3
ÉNONCÉ
Soit la matrice M =
. Déterminer sa matrice inverse M'.
1 2
ETAPE 1
Véri er que la matrice est carrée
On véri e que la matrice est carrée, c'est-à-dire qu'elle a le même nombre de lignes que de colonnes.
APPLICATION
La matrice M est carrée de dimension 2.
ETAPE 2
Poser une matrice de même dimension à coef cients indéterminés
On dé nit une matrice M' à coef cients indéterminés.
a b
APPLICATION
On pose M ′ = .
c d
Kartable.fr 1/3 Déterminer par le calcul une matrice inverse
Chapitre 4 Terminale S
Les matrices Déterminer par le calcul une matrice inverse Mathématiques
MM ′ = I
ETAPE 3
Poser
La matrice M' est inverse de la matrice M si et seulement si MM ′ = I .
On pose donc le calcul et on en déduit un système d'équations.
APPLICATION
On sait que MM ′ = I .
Donc :
1 3 a b 1 0
=
1 2 c d 0 1
D'où :
a + 3c b + 3d 1 0
=
a + 2c b + 2d 0 1
On en déduit le système suivant :
a + 3c = 1
b + 3d = 0
a + 2c = 0
b + 2d = 1
Kartable.fr 2/3 Déterminer par le calcul une matrice inverse
Chapitre 4 Terminale S
Les matrices Déterminer par le calcul une matrice inverse Mathématiques
ETAPE 4
Résoudre
On résout le système d'équations.
APPLICATION
On résout le système :
a + 3c = 1
b + 3d = 0
a + 2c = 0
b + 2d = 1
a + 3c = 1
b = −3d
⇔
a = −2c
b + 2d = 1
−2c + 3c = 1
b = −3d
⇔
a = −2c
−3d + 2d = 1
c = 1
b = −3d
⇔
a = −2c
d = −1
c = 1
b = 3
⇔
a = −2
d = −1
ETAPE 5
Conclure
On conclut en donnant M'.
APPLICATION
On conclut que M est inversible et que sa matrice inverse vaut :
−2 3
M′ =
1 −1
Kartable.fr 3/3 Déterminer par le calcul une matrice inverse
Chapitre 4 Terminale S
Les matrices Représenter une situation par une matrice Mathématiques
SITUATION
On peut représenter une situation par une matrice a n ensuite de pouvoir utiliser le calcul matriciel pour résoudre un
problème.
ÉNONCÉ
Une entreprise de restauration doit fournir cinq de ses restaurants en tables, chaises, banquettes et éclairage.
Le service comptable de l'entreprise a relevé les quantités des différents articles pour chaque restaurant.
Restaurant A : 15 tables, 40 chaises, 6 banquettes et 12 éclairages
Restaurant B : 22 tables, 8 chaises, 3 banquettes et 9 éclairages
Restaurant C : 32 tables, 50 chaises, 12 banquettes et 2 éclairages
Restaurant D : 43 tables, 55 chaises, 17 banquettes et 1 éclairages
Restaurant E : 8 tables, 28 chaises, 3 banquettes et 11 éclairages
Traduire ces données dans une matrice.
ETAPE 1
Écrire les données dans un tableau
On organise les données de l'énoncé dans un tableau.
APPLICATION
Les données de l'énoncé peuvent être récapitulées dans le tableau suivant :
Tables Chaises Banquettes Éclairages
Restaurant A 15 40 6 12
Restaurant B 22 8 3 9
Restaurant C 32 50 12 2
Restaurant D 43 55 17 1
Restaurant E 8 28 3 11
ETAPE 2
Transformer le tableau en matrice
On écrit le tableau sous forme de matrice.
APPLICATION
On peut donc représenter la situation par la matrice suivante :
15 40 6 12
22 8 3 9
A = 32 50 12 2
43 55 17 1
8 28 3 11
Kartable.fr 1/1 Représenter une situation par une matrice
Chapitre 4 Terminale S
Les matrices Résoudre un système linéaire en utilisant une Mathématiques
équation matricielle
SITUATION
Il est possible de résoudre facilement un système en l'écrivant sous forme matricielle. Il faut pour cela connaître la matrice
inverse de la matrice formée par les coef cients des inconnues.
1 1
ÉNONCÉ
3 3 1 1
Sachant que est la matrice inverse de
2 1 2 −1
, résoudre le système suivant :
−
3 3
x = 1 − y
2x − y − 2 = 0
ETAPE 1
Réduire la forme du système
On place toutes les inconnues dans les membres d...
Les matrices Déterminer par le calcul une matrice inverse Mathématiques
SITUATION
On peut déterminer l'inverse d'une matrice carrée M en la multipliant par une matrice carrée de même ordre à coef cients
inconnus et résolvant un système d'équations obtenu.
1 3
ÉNONCÉ
Soit la matrice M =
. Déterminer sa matrice inverse M'.
1 2
ETAPE 1
Véri er que la matrice est carrée
On véri e que la matrice est carrée, c'est-à-dire qu'elle a le même nombre de lignes que de colonnes.
APPLICATION
La matrice M est carrée de dimension 2.
ETAPE 2
Poser une matrice de même dimension à coef cients indéterminés
On dé nit une matrice M' à coef cients indéterminés.
a b
APPLICATION
On pose M ′ = .
c d
Kartable.fr 1/3 Déterminer par le calcul une matrice inverse
Chapitre 4 Terminale S
Les matrices Déterminer par le calcul une matrice inverse Mathématiques
MM ′ = I
ETAPE 3
Poser
La matrice M' est inverse de la matrice M si et seulement si MM ′ = I .
On pose donc le calcul et on en déduit un système d'équations.
APPLICATION
On sait que MM ′ = I .
Donc :
1 3 a b 1 0
=
1 2 c d 0 1
D'où :
a + 3c b + 3d 1 0
=
a + 2c b + 2d 0 1
On en déduit le système suivant :
a + 3c = 1
b + 3d = 0
a + 2c = 0
b + 2d = 1
Kartable.fr 2/3 Déterminer par le calcul une matrice inverse
Chapitre 4 Terminale S
Les matrices Déterminer par le calcul une matrice inverse Mathématiques
ETAPE 4
Résoudre
On résout le système d'équations.
APPLICATION
On résout le système :
a + 3c = 1
b + 3d = 0
a + 2c = 0
b + 2d = 1
a + 3c = 1
b = −3d
⇔
a = −2c
b + 2d = 1
−2c + 3c = 1
b = −3d
⇔
a = −2c
−3d + 2d = 1
c = 1
b = −3d
⇔
a = −2c
d = −1
c = 1
b = 3
⇔
a = −2
d = −1
ETAPE 5
Conclure
On conclut en donnant M'.
APPLICATION
On conclut que M est inversible et que sa matrice inverse vaut :
−2 3
M′ =
1 −1
Kartable.fr 3/3 Déterminer par le calcul une matrice inverse
Chapitre 4 Terminale S
Les matrices Représenter une situation par une matrice Mathématiques
SITUATION
On peut représenter une situation par une matrice a n ensuite de pouvoir utiliser le calcul matriciel pour résoudre un
problème.
ÉNONCÉ
Une entreprise de restauration doit fournir cinq de ses restaurants en tables, chaises, banquettes et éclairage.
Le service comptable de l'entreprise a relevé les quantités des différents articles pour chaque restaurant.
Restaurant A : 15 tables, 40 chaises, 6 banquettes et 12 éclairages
Restaurant B : 22 tables, 8 chaises, 3 banquettes et 9 éclairages
Restaurant C : 32 tables, 50 chaises, 12 banquettes et 2 éclairages
Restaurant D : 43 tables, 55 chaises, 17 banquettes et 1 éclairages
Restaurant E : 8 tables, 28 chaises, 3 banquettes et 11 éclairages
Traduire ces données dans une matrice.
ETAPE 1
Écrire les données dans un tableau
On organise les données de l'énoncé dans un tableau.
APPLICATION
Les données de l'énoncé peuvent être récapitulées dans le tableau suivant :
Tables Chaises Banquettes Éclairages
Restaurant A 15 40 6 12
Restaurant B 22 8 3 9
Restaurant C 32 50 12 2
Restaurant D 43 55 17 1
Restaurant E 8 28 3 11
ETAPE 2
Transformer le tableau en matrice
On écrit le tableau sous forme de matrice.
APPLICATION
On peut donc représenter la situation par la matrice suivante :
15 40 6 12
22 8 3 9
A = 32 50 12 2
43 55 17 1
8 28 3 11
Kartable.fr 1/1 Représenter une situation par une matrice
Chapitre 4 Terminale S
Les matrices Résoudre un système linéaire en utilisant une Mathématiques
équation matricielle
SITUATION
Il est possible de résoudre facilement un système en l'écrivant sous forme matricielle. Il faut pour cela connaître la matrice
inverse de la matrice formée par les coef cients des inconnues.
1 1
ÉNONCÉ
3 3 1 1
Sachant que est la matrice inverse de
2 1 2 −1
, résoudre le système suivant :
−
3 3
x = 1 − y
2x − y − 2 = 0
ETAPE 1
Réduire la forme du système
On place toutes les inconnues dans les membres d...












