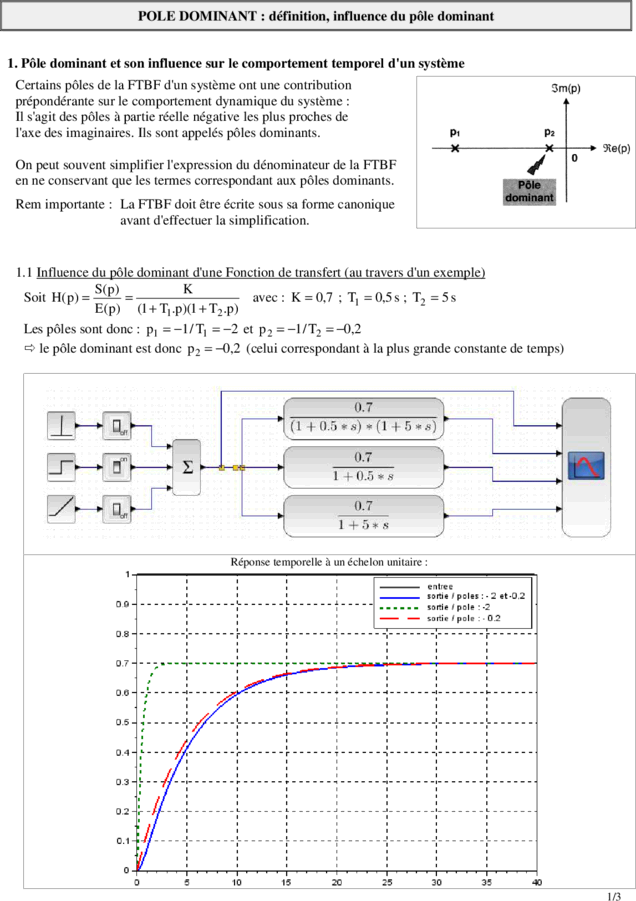
POLE DOMINANT : définition, influence du pôle dominant


1. Pôle dominant et son influence sur le comportement temporel d'un système
Certains pôles de la FTBF d'un système ont une contribution
prépondérante sur le comportement dynamique du système :
Il s'agit des pôles à partie réelle négative les plus proches de
l'axe des imaginaires. Ils sont appelés pôles dominants.

On peut souvent simplifier l'expression du dénominateur de la FTBF
en ne conservant que les termes correspondant aux pôles dominants.
Rem importante : La FTBF doit être écrite sous sa forme canonique
avant d'effectuer la simplification.


1.1 Influence du pôle dominant d'une Fonction de transfert (au travers d'un exemple)
S(p) K
Soit H(p) = = avec : K = 0,7 ; T1 = 0,5 s ; T2 = 5 s
E (p) (1 + T1 .p)(1 + T2 .p)
Les pôles sont donc : p1 = −1 / T1 = −2 et p 2 = −1 / T2 = −0,2
le pôle dominant est donc p 2 = −0,2 (celui correspondant à la plus grande constante de temps)




Réponse temporelle à un échelon unitaire :




1/3
Explication :
1 K K.T1 /(T2 − T1 ) K.T2 /(T1 − T2 )
2 2
K
S(p) = H(p).E(p) = . = + +
(1 + T1 .p)(1 + T2 .p) p p 1 + T1.p 1 + T2 .p

K K.T1 /(T2 − T1 ) K.T2 /(T2 − T1 )  1 T /(T − T1 ) T2 /(T2 − T1 ) 
S(p) = + − = K. + 1 2 − 
p p + 1 / T1 p + 1 / T2  p p + 1 / T1 p + 1 / T2 

 T1 T2 
s( t ) = K.1 + .e − t / T1 − .e − t / T2 
 T2 − T1 T2 − T1 

et si T1 suffisamment faible par rapport à T2 ( T1 << T2 ) :
T1 négligeable par rapport à T2
1 / T1 >> 1 / T2 e − t / T1 négligeable / e − t / T2 : ce dernier terme va imposer la décroissance exponentielle
(
s ( t ) ≃ K. 1 − e − t / T 2 )
 0,5 − 2 t 5 − 0 , 2 .t   5 −0,2.t 
Dans notre cas particulier : s( t ) = 0,7.1 + .e − .e  ≃ 0,7.1 − .e 
 4,5 4,5   4,5 
Conclusion :
Le terme e − t / T2 , correspondant au pôle dominant p 2 , devient prépondérant lorsque le temps croît et
détermine la dynamique asymptotique du système.

Rem :
sur l'exemple les pôles sont réels. Dans le cas de pôles complexes, il en est de même avec comme pôle
dominant celui ayant la partie réelle la plus faible.
on peut également mettre en évidence l'influence prépondérante du pôle dominant sur les diagrammes de Bode :
0,7 0,7
(1 + 0,5.p)(1 + 5.p) 1 + 5.p

ωc − 3dB ωc − 3dB




ωc 2 = 1 / 5 = 0, 2 rad/s ωc1 = 1 / 0,5 = 2 rad/s ωc 2 = 1 / 5 = 0, 2 rad/s




Comparaison des diagrammes de Bode du gain :
Aux faibles et moyennes pulsations (jusqu'à environ un peu au-delà de la première pulsation de cassure ωc 2 )
les diagrammes de Bode du gain sont quasi identiques, d'où :
pulsations de coupure à -3dB *quasi identiques même rapidité
gain identique à basse fréquence même précision
* ωc − 3dB = g dB maxi − 3dB = 20. log 0,7 − 3dB
2/3
1.2 Influence du pôle dominant de la FTBO sur la FTBF :
K
On considère un système bouclé à retour unitaire de FTBO telle que : FTBO(p) =
(1 + T1 .p)(1 + T2 .p)
FTBO(p) 1 1 K
FTBF(p) = = = =
1 + FTBO(p) 1 (1 + T1 .p)(1 + T2 .p) K + (1 + T1 .p)(1 + T2 .p)
1+ 1+
FTBO(p) K
K
FTBF(p) =
K
= 1+ K
(K + 1) + (T1 + T2 ).p + T1.T2 .p 2 T + T T .T
1+ 1 2
.p + 1 2 .p 2
1+ K 1+ K
K
et si T1 suffisamment faible par rapport à T2 : FTBF(p) ≃ 1 + K
T
1 + 2 .p
1+ K
On aurait obtenu le même résultat en ne prenant en compte que le pôle dominant de la FTBO :
K
= 1+ K
K 1 1 K
FTBO(p) ≃ FTBF(p) = = =
1 + T2 .p 1 1 + T .p K + 1 + T2 .p T
1+ 1+ 2
1 + 2 .p
FTBO(p) K 1+ K

Conclusion : le pôle dominant de la FTBO p 2 = −1 / T2 est également prépondérant sur la FTBF.




Réponse temporelle à un échelon unitaire :




...




3/3