Formulaire système de coordonnées
File hierarchy
| Downloads | ||||||
| Files created online | (28979) | |||||
| TI-Nspire | (20931) | |||||
| mViewer GX Creator Ndless | (940) | |||||
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Ndless TI-Nspire
Auteur Author: yoppyop
Type : Image nécessitant un lecteur
Page(s) : 1
Taille Size: 57.60 Ko KB
Mis en ligne Uploaded: 13/01/2015 - 19:59:33
Uploadeur Uploader: yoppyop (Profil)
Téléchargements Downloads: 172
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a137052
Type : Image nécessitant un lecteur
Page(s) : 1
Taille Size: 57.60 Ko KB
Mis en ligne Uploaded: 13/01/2015 - 19:59:33
Uploadeur Uploader: yoppyop (Profil)
Téléchargements Downloads: 172
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a137052
Description
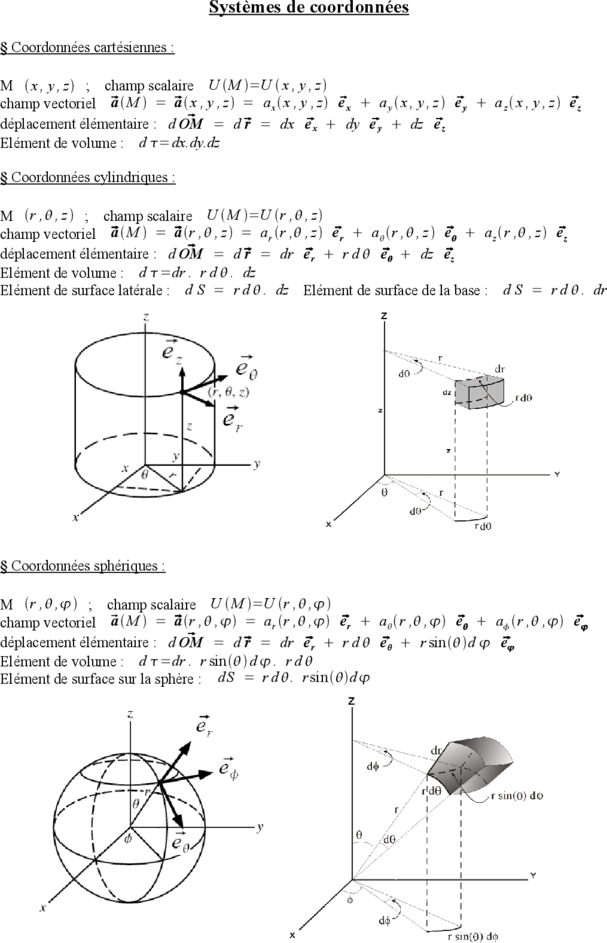
Systèmes de coordonnées
§ Coordonnées cartésiennes :
M x , y , z ; champ scalaire U M =U x , y , z
champ vectoriel a M = a x , y , z = a x x , y , z ex a y x , y , z ey a z x , y , z ez
déplacement élémentaire : d OM = d r = dx ex dy ey dz ez
Elément de volume : d =dx.dy.dz
§ Coordonnées cylindriques :
M r , , z ; champ scalaire U M =U r , , z
champ vectoriel a M = a r , , z = a r r , , z er a r , , z e a z r , , z ez
déplacement élémentaire : d OM = d r = dr er r d e dz ez
Elément de volume : d =dr . r d . dz
Elément de surface latérale : d S = r d . dz Elément de surface de la base : d S = r d . dr
§ Coordonnées sphériques :
M r , , ; champ scalaire U M =U r , ,
champ vectoriel a M = a r , , = a r r , , er a r , , e a r , , e
déplacement élémentaire : d OM = d r = dr er r d e r sind e
Elément de volume : d =dr . r sin d . r d
Elément de surface sur la sphère : d S = r d . r sin d
§ Coordonnées cartésiennes :
M x , y , z ; champ scalaire U M =U x , y , z
champ vectoriel a M = a x , y , z = a x x , y , z ex a y x , y , z ey a z x , y , z ez
déplacement élémentaire : d OM = d r = dx ex dy ey dz ez
Elément de volume : d =dx.dy.dz
§ Coordonnées cylindriques :
M r , , z ; champ scalaire U M =U r , , z
champ vectoriel a M = a r , , z = a r r , , z er a r , , z e a z r , , z ez
déplacement élémentaire : d OM = d r = dr er r d e dz ez
Elément de volume : d =dr . r d . dz
Elément de surface latérale : d S = r d . dz Elément de surface de la base : d S = r d . dr
§ Coordonnées sphériques :
M r , , ; champ scalaire U M =U r , ,
champ vectoriel a M = a r , , = a r r , , er a r , , e a r , , e
déplacement élémentaire : d OM = d r = dr er r d e r sind e
Elément de volume : d =dr . r sin d . r d
Elément de surface sur la sphère : d S = r d . r sin d












