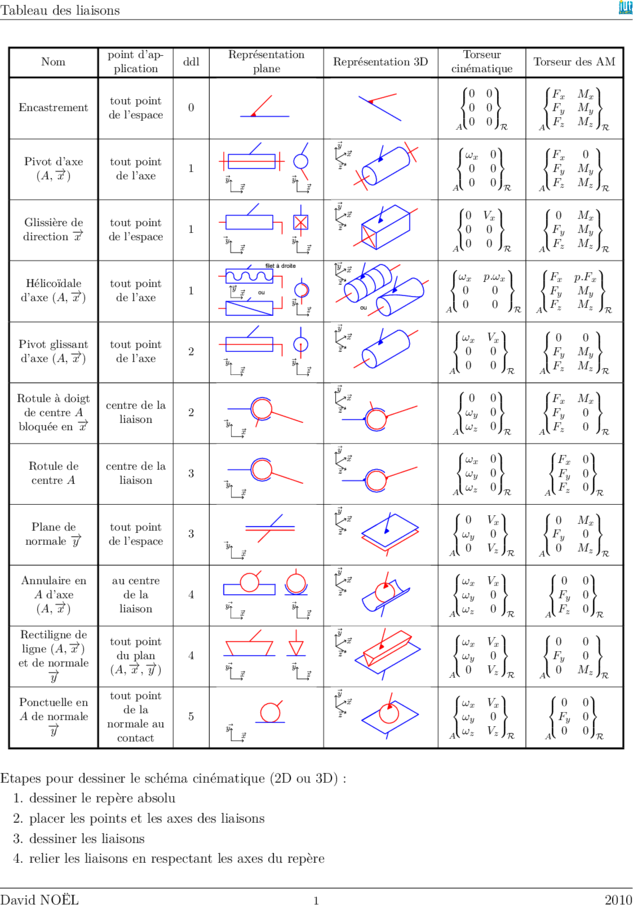
Tableau des liaisons


point d’ap- Représentation Torseur
Nom ddl Représentation 3D Torseur des AM
plication plane cinématique
   
0 0 Fx Mx 
tout point
Encastrement 0 0 0 Fy My
de l’espace
0 0 R Fz Mz R
   
A A

y    
x ωx 0  Fx 0 
Pivot d’axe tout point
1 z 0 0 Fy My
(A, →
−
x) de l’axe y y
0 0 R Fz Mz R
   
x z A A

y    
x 0 Vx  0 Mx 
Glissière de tout point z
1 0 0 Fy My
direction →
−x de l’espace y y
0 0 R Fz Mz R
   
x z A A
filet à droite y x    
ωx p.ωx  Fx p.Fx 
Hélicoïdale tout point y
z
1 0 0 Fy My
d’axe (A, →
− x ou
x) de l’axe y 0 0 R Fz Mz R
   
ou
z A A

y    
x ωx Vx  0 0 
Pivot glissant tout point z
2 0 0 Fy My
d’axe (A, →−
x) de l’axe y y
0 0 R Fz Mz R
   
x z A A

y    
Rotule à doigt x 0 0 Fx Mx 
centre de la
de centre A 2 z ωy 0 Fy 0
liaison
bloquée en →
−x y ωz 0 R Fz 0 R
   
x A A

y    
x ωx 0 Fx 0
Rotule de centre de la
3 z ωy 0 Fy 0
centre A liaison y ωz 0 R Fz 0 R
   
x A A

y    
x 0 Vx  0 Mx 
Plane de tout point
3 z ωy 0 Fy 0
normale →
−
y de l’espace y 0 Vz R 0 Mz R
   
x A A

y    
Annulaire en au centre x ωx Vx  0 0
A d’axe de la 4 z ωy 0 Fy 0
(A, →
−
x) liaison y y
ωz 0 R Fz 0 R
   
x z A A

Rectiligne de y    
tout point x ωx Vx  0 0 
ligne (A, →
−
x)
du plan 4 z ωy 0 Fy 0
et de normale
(A, →
−
x,→−
y) y y
0 Vz R 0 Mz R
 
→
−
 
y x z A A

tout point y    
Ponctuelle en x ωx Vx  0 0
de la
A de normale 5 z ωy 0 Fy 0
→
− normale au y
y ωz Vz R 0 0 R
   
contact x A A




Etapes pour dessiner le schéma cinématique (2D ou 3D) :
1. dessiner le repère absolu
2. placer les points et les axes des liaisons
3. dessiner les liaisons
4. relier les liaisons en respectant les axes du repère

David NOËL 1 2010
 Modélisation des liaisons
Compétences associées
B2 : Construire un modèle et le représenter à l’aide
de schémas.
Établir la réciprocité mouvement relatif / actions
mécaniques mécaniques associées
Construire un graphe de liaisons



La Mécanique est un outil de travail qui peut s’utiliser dans deux démarches essentielles lors du cycle de vie des
produits industriels :

Dans une phase d’analyse d’un objet technique existant, l’outil « mécanique » permet de quantifier certaines
grandeurs physiques, de mettre en évidence certaines propriétés, et surtout de justifier ou d’améliorer certaines
solutions technologiques du produit étudié.


Dans la démarche de conception les principes de la mécanique permettent de prévoir des événements physiques,
d’optimiser des formes, de déterminer des dimensions alors que le produit n’existe pas encore.

La réalité d’un mécanisme étant trop complexe, il est nécessaire d’en élaborer une image plus ou moins simplifiée,
avant d’utiliser les principes ou les lois de la mécanique. Une démarche de modélisation des grandeurs réelles
s’impose donc. On associe généralement à ces modèles une représentation graphique sous forme de schéma.

Le choix d’un modèle porte sur des grandeurs de deux types :

Grandeurs géométriques (nature des surfaces, valeurs des jeux etc.)
Grandeurs physiques comme les actions mécaniques, les paramètres cinématiques ou ceux utilisés pour
caractériser les propriétés intrinsèques d’un matériau.


MODELISATION DES SOLIDES ET DES SYSTEMES MATERIELS
NOTION DE MODELE
C’est une abstraction de la réalité qui ressemble suffisamment à l’objet modélisé.

LE SOLIDE
Le solide REEL est celui que l’on trouve dans notre environnement ; il est déformable, non homogène de par
sa structure cristalline et ses caractéristiques mécaniques peuvent varier avec le temps. Cette multitude de
paramètres difficilement quantifiables impose d’associer un modèle à ce corps solide.

SOLIDE GEOMETRIQUE
Définition : soit S un ensemble de points. S est un solide géométrique si et seulement M
si, quelque soit les points M, N et P appartenant à S, nous avons :
N P
MN=Cste MP = Cste PN=Cste
(S)


Z

Y

A chaque solide géométrique S, on peut associer un repère
O orthonormé direct
SSII MERMOZ




Repère associé à un solide
X
géométrique
Modélisation des liaisons mécaniques Page 1 sur 5
 CARACTERISTIQUES DU REPERE :
 méthode du tir bouchon
Représentation Z Représentations dans le plan  méthode des « 3 doigts »
d’un repère
dans l’espace Y Z Z

O 1
1 1
O O O
X Y
Z X X Y Y X

NOTION DE DEGRE DE LIBERTE
Lors de mouvements quelconques entre solides, on peut décomposer Z
celui-ci en plusieurs mouvements élémentaires :
RZ
Sur chacun des trois axes ( O, x ) , ( O, y ) et ( O, z ) , il y a deux types de TZ
mouvements possibles :
RX TX TY RY
UNE TRANSLATION
UNE ROTATION

Définition : On appelle degré de liberté la liberté de mouvement en X Y
rotation ou en translation d'un solide par rapport à l'autre solide.

Nombre maxi de degrés de liberté : 6


DEFINITIONS RELATIVES AUX LIAISONS ENTRE SOLIDES
A l’intérieur des mécanismes industriels, on rencontre des corps solides dont la nature des contacts mutuels
induit des particularités sur les mouvements possibles entre eux.
Définition d’une liaison : Une liaison est une relation de contact entre deux solides.

LES DIFFERENTS TYPES DE CONTACT
Les solides étudiés dans ce chapitre sont supposés indéformables. On distingue de manière purement
théorique trois grands types de contact :

Le contact ponctuel Le contact linéaire Le contact surfacique
SSII MERMOZ




Modélisation des liaisons mécaniques Page 2 sur 5
 MODELISATION DES LIAISONS PRINCIPALES
A chaque contact autorisant des déplacements entre deux systèmes matériels notés (1) et (2), sera mis en
évidence un repère qui permet d’exprimer simplement les propriétés de ce contact : on l’appelle repère
local. Il est également lié à un des systèmes matériels concernés par ce contact.
L’origine du repère local est un point privilégié de la surface de contact.
L’axe principal correspond à l’axe de symétrie privilégié de la surface de contact s’il existe. Les deux autres
axes sont tels que le repère soit orthonormé de sens direct.
Pour les liaisons qui suivent, les déplacements élémentaires du système (2) par rapport au système (1) et le
repère local seront indiqués dans un tableau.


LIAISON PONCTUELLE
z z
z

y
T R
x 1 1
y 1 1 x x
x y x y
z 0 1



LIAISON LINEAIRE RECTILIGNE
z z
z z
T R
x 1 1
y 1 0 x y
x y
z 0 1 x y



LIAISON LINEAIRE ANNULAIRE
z z z
z