Soit une suite définie par :
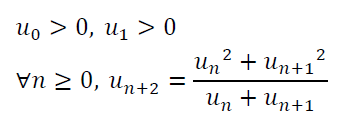
En introduisant une série, montrer que la suite (un) converge.
1. Je démontre facilement que (un) est une suite à termes strictement positifs.
2. Je calcule u(n+2)-u(n+1),
j'obtiens u(n+2)-u(n+1) = -u(n) * (u(n+1)-u(n)) * 1/(u(n) + u(n+1)).
J'en déduis que pour tout n = 2, on peut écrire u(n) sous la forme :
u(n) = u(1) + somme pour k allant de 2 à n de (-u(k-2) * (u(k-1) - u(k-2))/(u(k-2) + u(k-1)))
u(n) = u(1) + somme pour k allant de 2 à n de ((-1)^k * u(k-2) * |u(k-1) - u(k-2)|/(u(k-2) + u(k-1))),
le (-1)^k pouvant être remplacé par (-1)^(k+1) selon les cas.
3. Je tenterais bien de prouver que u(k-2) * |u(k-1) - u(k-2)|/(u(k-2) + u(k-1)) décroît quand k augmente, mais je sèche...
Une idée ?
























