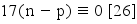On a le système
5a+b (congru à) 10 (modulo) 26
19a+b (congru à) 14 (modulo) 26
J'en ai déduit (d'après la question) qu'il existe un entier k tel que 14a-26k=4
J'ai déjà résolu cette équation auparavant, les solutions sont de la forme
a=4+26n
k=2+14n
n étant un entier relatif
Et la question qui pose problème :
"Déterminer tous les couples d'entiers (a,b), avec 0=a=25 et 0=b=25, tels que
5a+b (congru à) 10 (modulo) 26
19a+b (congru à) 14 (modulo) 26
A l'aide d'un programme (héhé ça sert) j'ai trouvé 2 solutions :
a=4 et b=16 ou a=17 et b=3
Pour la première c'est "logique", mais pour la 2ème ??
merci





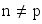 ) telles qu'elles soient codées par la même lettre.
) telles qu'elles soient codées par la même lettre.