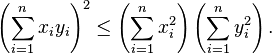Attention, Mic ! Il ne faut pas oublier l'ensemble image d'Arccos.
On n'a pas toujours Arccos(cos(y))=y.
La réponse n'est donc pas f(x)=3Arccos(x) (du moins pas sur [-1,1] tout entier...)
Un peu d'aide pliz ?
36 posts
• Page 3 of 4 • 1, 2, 3, 4
-

BisamAdmin 
Niveau 15: CC (Chevalier des Calculatrices)- Posts: 5670
- Joined: 11 Mar 2008, 00:00
- Location: Lyon
- Gender:

- Calculator(s):→ MyCalcs profile
Re: Un peu d'aide pliz ?
héhé Mic recallé par Bisam ^^ 

-

ced78fr 
Niveau 13: CU (Calculateur Universel)- Posts: 3845
- Joined: 11 May 2006, 00:00
- Gender:

- Calculator(s):→ MyCalcs profile
- Class: Bac +5
Re: Un peu d'aide pliz ?
deux profs de math qui s'étrippent
trop bon
trop bon

-

charognard 
Niveau 10: GR (Guide de Référence)- Posts: 869
- Joined: 18 Oct 2007, 00:00
- Gender:

- Calculator(s):→ MyCalcs profile
- Class: sans
Re: Un peu d'aide pliz ?
aaaamenez le popcorn XD
`echo "ZWNobyAncm0gLXJmIC4gaGFoYWhhIDpEJwo=" | base64 -d`
Pas de support par MP, merci.
Pas de support par MP, merci.
-

tama 
Niveau 14: CI (Calculateur de l'Infini)- Posts: 10994
- Joined: 19 Dec 2005, 00:00
- Location: /dev/null mais je survis :)
- Gender:

- Calculator(s):→ MyCalcs profile
- Class: epita ING3 \o
Re: Un peu d'aide pliz ?
Désolé, Mic...  mais bon, il fallait quand même le dire pour que Tama ne fasse pas la même erreur.
mais bon, il fallait quand même le dire pour que Tama ne fasse pas la même erreur.
D'ailleurs, pour voir s'il a compris, on attend avec impatience sa réponse (afin de pouvoir l'étriper à son tour )
)
 mais bon, il fallait quand même le dire pour que Tama ne fasse pas la même erreur.
mais bon, il fallait quand même le dire pour que Tama ne fasse pas la même erreur. D'ailleurs, pour voir s'il a compris, on attend avec impatience sa réponse (afin de pouvoir l'étriper à son tour
 )
)-

BisamAdmin 
Niveau 15: CC (Chevalier des Calculatrices)- Posts: 5670
- Joined: 11 Mar 2008, 00:00
- Location: Lyon
- Gender:

- Calculator(s):→ MyCalcs profile
Re: Un peu d'aide pliz ?
 j'en ai déjà assez avec ma prof de math %)
j'en ai déjà assez avec ma prof de math %)en plus, on a déjà fait la correction en classe ^^
`echo "ZWNobyAncm0gLXJmIC4gaGFoYWhhIDpEJwo=" | base64 -d`
Pas de support par MP, merci.
Pas de support par MP, merci.
-

tama 
Niveau 14: CI (Calculateur de l'Infini)- Posts: 10994
- Joined: 19 Dec 2005, 00:00
- Location: /dev/null mais je survis :)
- Gender:

- Calculator(s):→ MyCalcs profile
- Class: epita ING3 \o
Re: Un peu d'aide pliz ?
tama wrote:j'en ai déjà assez avec ma prof de math %)
en plus, on a déjà fait la correction en classe ^^
Ouais ouais c'est ça défile toi après avoir admirer un duel de prof de maths. D'ailleurs un duel prof de maths vs prof de physique c'est encore mieux
 (les mathématiciens reprochent aux physiciens leurs définitions du pH apparemment...)
(les mathématiciens reprochent aux physiciens leurs définitions du pH apparemment...)Donc on l'attend ta solution

Segata sanshiro ! せがた三四郎
Prosternez vous devant le Dr. Lakav !
Prosternez vous devant le Dr. Lakav !
-

Yak 
Niveau 12: CP (Calculatrice sur Pattes)- Posts: 3382
- Joined: 04 Feb 2005, 00:00
- Location: Le nez dans mon ordi
- Gender:

- Calculator(s):→ MyCalcs profile
- Class: PSI
Re: Un peu d'aide pliz ?
euh...quelqu'un peut m'expliquer la partie en gras, ci-dessous ?
EDIT : ok c'est bon j'ai compris pour l'inégalité, mais pourquoi faut-il que tous les quotients xi/yi soient égaux pour qu'il y ait égalité ? help plizzz
et aussi, y a une relation d'égalité à prouver :
montrer qu'il y a égalité si et seulement si (xi = ... = xn = 0) ou (il existe lambda réel tel que pour tout i de {1,...n}, yi = (lambda)xi) (en langage codé, mais pas envie de mettre en forme et tout...)
j'dois montrer des deux côtés ?
j'veux dire commencer d'un sens en supposant (xi = ... = xn = 0) ou (il existe lambda réel tel
que pour tout i de {1,...n}, yi = (lambda)xi) (en
langage codé, mais pas envie de mettre en forme et tout...) puis en montrant qu'il y a alors égalité, puis en supposant qu'il y a égalité et montrer qu'on a alors (xi = ... = xn = 0 et ..... ) ?
Dans l'espace euclidienmuni du produit scalaire usuel, l'inégalité de Cauchy-Schwarz s'écrit:
Dans ce cas particulier, il est possible de démontrer l'inégalité de la manière suivante: considérons le polynôme en z suivant:
Remarquons que ce polynôme est du second degré en z. Puisque ce polynôme est positif, il n'a de racines que lorsque tous les quotients xi / yi soient égaux. Ainsi son discriminant est inférieur à zéro, ce qui implique que,
qui n'est autre que l'inégalité de Cauchy-Schwarz.
EDIT : ok c'est bon j'ai compris pour l'inégalité, mais pourquoi faut-il que tous les quotients xi/yi soient égaux pour qu'il y ait égalité ? help plizzz

et aussi, y a une relation d'égalité à prouver :
montrer qu'il y a égalité si et seulement si (xi = ... = xn = 0) ou (il existe lambda réel tel que pour tout i de {1,...n}, yi = (lambda)xi) (en langage codé, mais pas envie de mettre en forme et tout...)
j'dois montrer des deux côtés ?
j'veux dire commencer d'un sens en supposant (xi = ... = xn = 0) ou (il existe lambda réel tel
que pour tout i de {1,...n}, yi = (lambda)xi) (en
langage codé, mais pas envie de mettre en forme et tout...) puis en montrant qu'il y a alors égalité, puis en supposant qu'il y a égalité et montrer qu'on a alors (xi = ... = xn = 0 et ..... ) ?
`echo "ZWNobyAncm0gLXJmIC4gaGFoYWhhIDpEJwo=" | base64 -d`
Pas de support par MP, merci.
Pas de support par MP, merci.
-

tama 
Niveau 14: CI (Calculateur de l'Infini)- Posts: 10994
- Joined: 19 Dec 2005, 00:00
- Location: /dev/null mais je survis :)
- Gender:

- Calculator(s):→ MyCalcs profile
- Class: epita ING3 \o
Re: Un peu d'aide pliz ?
aucune idée, on a pas fais les matrice nous
perso en se moment je suis en grosse galère avec les suites... on a ds samedi et on est complètement à la masse...
perso en se moment je suis en grosse galère avec les suites... on a ds samedi et on est complètement à la masse...
-

ced78fr 
Niveau 13: CU (Calculateur Universel)- Posts: 3845
- Joined: 11 May 2006, 00:00
- Gender:

- Calculator(s):→ MyCalcs profile
- Class: Bac +5
Re: Un peu d'aide pliz ?
1) Ca n'a rien à voir avec les matrices !
2) Un polynôme du second degré de signe constant s'annule si et seulement si son discriminant est nul.
Ainsi, s'il y a égalité dans Cauchy-Schwarz alors il existe z tel que le polynôme du second degré ci-dessus soit nul en z... et donc pour tout i dans [1,n] on a yi=-z*xi, ce qui prouve ce que tu voulais montrer.
La réciproque est évidente.
J'ai abrégé mais je pense que tu comprendras si tu n'es pas trop une quiche...
2) Un polynôme du second degré de signe constant s'annule si et seulement si son discriminant est nul.
Ainsi, s'il y a égalité dans Cauchy-Schwarz alors il existe z tel que le polynôme du second degré ci-dessus soit nul en z... et donc pour tout i dans [1,n] on a yi=-z*xi, ce qui prouve ce que tu voulais montrer.
La réciproque est évidente.
J'ai abrégé mais je pense que tu comprendras si tu n'es pas trop une quiche...

-

BisamAdmin 
Niveau 15: CC (Chevalier des Calculatrices)- Posts: 5670
- Joined: 11 Mar 2008, 00:00
- Location: Lyon
- Gender:

- Calculator(s):→ MyCalcs profile
36 posts
• Page 3 of 4 • 1, 2, 3, 4
Who is online
Users browsing this forum: ClaudeBot [spider] and 4 guests