by ![>:]](./images/smilies/devilish.png "Devil")
mais voila un excellent problème pour vous casser la tête (GG a Ruadh qui a été le premier a donner un résultat qui semble fonctionner, cependant on a pas encore prouvé que ça fonctionne pour tout les cas (ça marche pour tout les cas qu'on a pu tester))Connaissez vous l'éponge de menger ?
Non ?
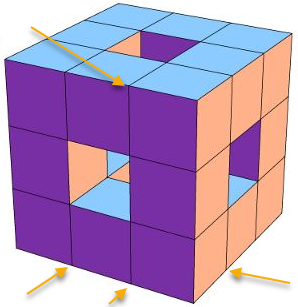
C'est tout simple: prenez un cube.
Dupliquez le de manière a avoir un cube plus gros de 3x3x3 fois ce cube, puis supprimez les cubes au centre de chaque face, ainsi que le cube central.
Vous obtiendrez ceci:
Vous répetez ces étapes (a partir de la duplication) en prenant ceci comme "cube" de départ.
L'éponge de menger, c'est tout simplement la fractale que vous obtiendrez après une infinité d'étapes.
Bon, c'est bien joli tout ça, mais ce serait intéressant de se demander "Mais dis donc Jamy, combien de sommets cette forme comporte-t-elle ?"
Bon, vous imaginez bien qu'avec une infinité d'étapes, y'a une infinité de sommets
Non, ce qui compte ici c'est le nombre de sommets a une étape donnée, ce qui nous donne une suite u(n) définie dans l'ensemble des entiers naturels, avec u(0) = 8 (bah oui, un cube ça a 8 sommets)
Bon, pour l'étape n°1, il suffit de compter (ou de lire le nombre de sommets affiché par votre logiciel
), et on trouve 64 (pour ceux qui seraient pas d'accord, je compte de cette manière :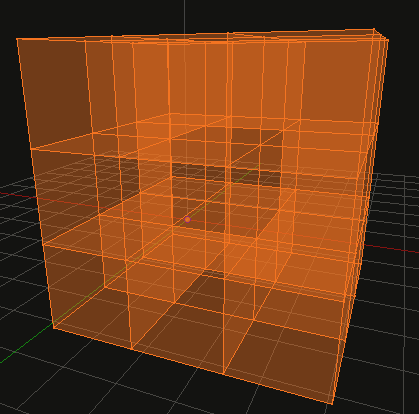
).A partir de la, on a donc
u(0) = 8
u(1) = 64
Et je vous épargne un peu le travail en ayant déjà trouvé un ptit bout du reste
u(2) = 896
u(3) = 15616
u(4) = 295808
Et merci a @IAMISSAM pour avoir prêté son ordi a la science
et avoir généré u(5)u(5) = 5789440
Voila, maintenant reste plus qu'a trouver la formule pour calculer u(n) sans avoir a compter soi même...
Bon, si on part du début, on prends notre cube de départ ( la valeur u(n) ) et on la multiplie par 27, puis on l'enlève 7 fois (du coup si u(n) vaut 8, on le multiplie par 20 (oui, 27-7=20) et on obtient 160). Cependant, si on reste comme ça, il y a des sommets qui se superposent (certains sommets de deux cubes adjacents, par exemple), il faut donc les enlever (dans notre cas, pour arriver a 64, il faut enlever 96 sommets). Du coup on en est a u(n+1) = 20*u(n)-x
Reste plus qu'a trouver comment calculer x pour avoir la formule au complet...
Encore une fois je vous donne les valeurs trouvées a la main:
u(0) = 8
u(1) = u(0)*20-96 = 64
u(2) = u(1)*20-384 = 896
u(3) = u(2)*20-2304 = 15616
u(4) = u(3)*20-16512 = 295808
Encore merci a @IAMISSAM pour u(5)
u(5) = u(4)*20-126720 = 5789440
Voilà voilà, je suis pas arrivé plus loin (a part avoir trouvé que 96 = u(0)*20-u(0)*8 et 384 = (u(1)*20 - u(1)*8)/2 ).
Donc voilà, je vous laisse vous casser le cerveau sur ce problème.... (je rappelle la consigne une dernière fois, il faut trouver la formule permettant de trouver u(n+1) a partir de tout ce que vous voulez (u(n), u(n-1), n, u(0),... ).
Bonne chance
)
