Méthodes
DownloadTélécharger
Actions
Vote :
ScreenshotAperçu
Informations
Catégorie :Category: mViewer GX Creator Lua TI-Nspire
Auteur Author: solerem
Type : Classeur 3.6
Page(s) : 7
Taille Size: 240.10 Ko KB
Mis en ligne Uploaded: 03/11/2018 - 13:41:29
Uploadeur Uploader: solerem (Profil)
Téléchargements Downloads: 55
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a1770242
Type : Classeur 3.6
Page(s) : 7
Taille Size: 240.10 Ko KB
Mis en ligne Uploaded: 03/11/2018 - 13:41:29
Uploadeur Uploader: solerem (Profil)
Téléchargements Downloads: 55
Visibilité Visibility: Archive publique
Shortlink : https://tipla.net/a1770242
Description
Chapitre 3 Terminale S
Les nombres premiers Le crible d'Érathostène Mathématiques
SITUATION
Le crible d'Eratosthène permet de trouver tous les nombres premiers plus petits qu'un entier naturel N prédé ni.
ÉNONCÉ
À l'aide du crible d'Eratosthène, déterminer tous les nombres premiers inférieurs à 100.
ETAPE 1
Écrire la liste de tous les nombres inférieurs à N
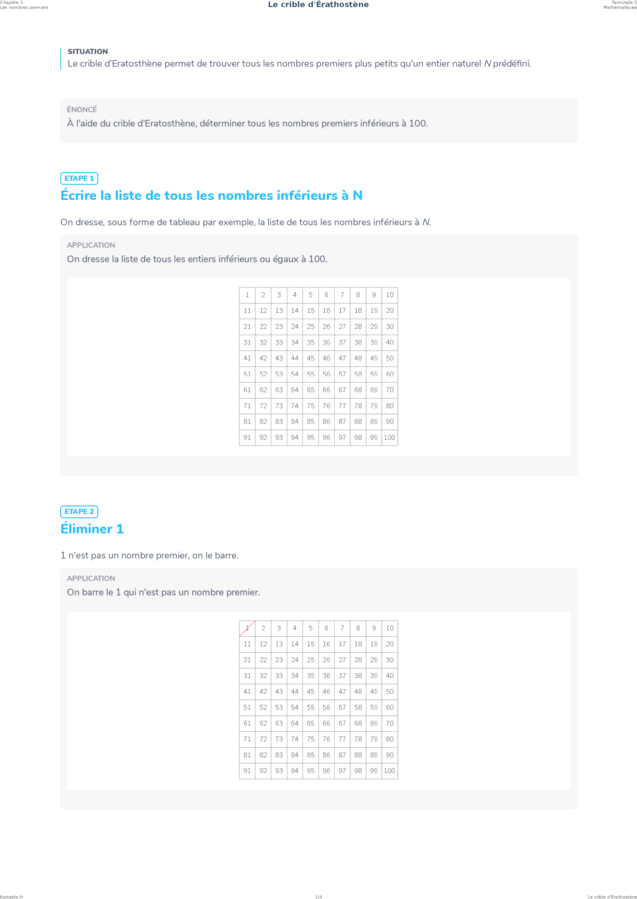
On dresse, sous forme de tableau par exemple, la liste de tous les nombres inférieurs à N.
APPLICATION
On dresse la liste de tous les entiers inférieurs ou égaux à 100.
ETAPE 2
Éliminer 1
1 n'est pas un nombre premier, on le barre.
APPLICATION
On barre le 1 qui n'est pas un nombre premier.
Kartable.fr 1/4 Le crible d'Érathostène
Chapitre 3 Terminale S
Les nombres premiers Le crible d'Érathostène Mathématiques
ETAPE 3
Entourer 2 et éliminer les multiples de 2
2 est le premier nombre premier, on l'entoure.
Tous les multiples de 2 ne peuvent donc pas être premiers, on les barre.
APPLICATION
On entoure le 2 et on barre les multiples de 2.
ETAPE 4
Entourer 3 et éliminer les multiples de 3
Dans le tableau, on sélectionne le premier nombre suivant qui n'a pas été barré. Ce nombre est premier. Ici, 3 est le nombre
premier suivant, on l'entoure.
Tous les multiples de 3 ne peuvent donc pas être premiers, on les barre.
APPLICATION
On entoure le 3 et on barre les multiples de 3.
Kartable.fr 2/4 Le crible d'Érathostène
Chapitre 3 Terminale S
Les nombres premiers Le crible d'Érathostène Mathématiques
ETAPE 5
Entourer 5 et éliminer les multiples de 5
Dans le tableau, on sélectionne le premier nombre suivant qui n'a pas été barré. Ce nombre est premier. Ici, 5 est le nombre
premier suivant, on l'entoure.
Tous les multiples de 5 ne peuvent donc pas être premiers, on les barre.
APPLICATION
À l'aide de la liste, le nombre premier suivant est le 5. On l'entoure et on barre les multiples de 5.
ETAPE 6
⎯⎯
⎯
Renouveler le procédé jusqu'à la partie entière de √N
On réitère le procédé avec tous les nombres premiers inférieurs ou égaux à √⎯⎯N⎯ .
APPLICATION
À l'aide de la liste, le nombre premier suivant est le 7. On l'entoure et on barre les multiples de 7.
Ensuite le nombre premier suivant est le 11. Or 11 > √⎯100
⎯⎯⎯⎯⎯.
Donc on s'arrête là.
Kartable.fr 3/4 Le crible d'Érathostène
Chapitre 3 Terminale S
Les nombres premiers Le crible d'Érathostène Mathématiques
ETAPE 7
Conclure
On conclut en donnant la liste des nombres non barrés de la liste : ce sont les nombres premiers inférieurs à N.
APPLICATION
Les nombres premiers inférieurs à 100 sont donc :
2 − 3 − 5 − 7 − 11 − 13 − 17 − 19 − 23 − 29 − 31 − 37 − 41 −
43 − 47 − 53 − 59 − 61 − 67 − 71 − 73 − 79 − 83 − 89 − 97
Kartable.fr 4/4 Le crible d'Érathostène
Chapitre 3 Terminale S
Les nombres premiers Recherche des diviseurs d'un nombre grâce à sa Mathématiques
décomposition en produit de nombres premiers
SITUATION
A n de déterminer tous les diviseurs d'un entier n, on le décompose en produit de facteurs premiers.
ÉNONCÉ
Rechercher tous les diviseurs de 120.
ETAPE 1
Décomposer l'entier en produit de facteurs premiers
On décompose n en produit de facteurs premiers.
APPLICATION
La décomposition de 120 en produit de facteurs premiers est :
120 = 23 × 3 × 5
ETAPE 2
Lister tous les diviseurs
On liste tous les diviseurs de l'entier n. On pourra notamment s'aider d'un arbre.
APPLICATION
Les diviseurs de 120 seront donc tous de la forme : 2m × 3n × 5p avec :
m ∈ {0;1;2;3}, soit 4 choix pour m
n ∈ {0;1}, soit 2 choix pour n
p ∈ {0;1}, soit 2 choix pour p
A n de dresser la liste complète des diviseurs de 120, on dresse l'arbre ci-dessous :
ETAPE 3
Conclure
On conclut en donnant l'ensemble des diviseurs de n.
APPLICATION
On en conclut que l'ensemble des diviseurs de 120 est :
{1;2;3;4;5;6;8;10;12;15;20;24;30;40;60;120}
Kartable.fr 1/1 Recherche des diviseurs d'un nombre grâce à sa décomposition en produit de nombres premiers
Chapitre 3 Terminale S
Les nombres premiers Recherche du nombre de diviseurs d'un entier Mathématiques
naturel
n = ap × bq × cr possède (p + 1) × (q + 1) × (r + 1) diviseurs.
SITUATION
L'entier n dont la décomposition en facteurs premiers est
ÉNONCÉ
Déterminer le nombre de diviseurs de l'entier 720.
ETAPE 1
Décomposer n en produit de facteurs premiers
On décompose n en produit de facteurs premiers.
APPLICATION
La décomposition en produit de facteurs premiers de 720 est :
720 = 24 × 32 × 5
ETAPE 2
Réciter le cours
D'après le cours, on sait que le nombre de diviseurs d'un entier n est le produit des exposants apparaissant dans sa
décomposition en facteurs premiers, chacun augmenté de 1.
Ainsi l'entier n dont la décomposition en facteurs premiers est n = ap × bq × cr a (p + 1) × (q + 1) × (r + 1) diviseurs.
APPLICATION
Le nombre de diviseurs d'un entier n est le produit des puissances apparaissant dans sa décomposition en facteurs
premiers, chacune augmentée de 1.
ETAPE 3
...
Les nombres premiers Le crible d'Érathostène Mathématiques
SITUATION
Le crible d'Eratosthène permet de trouver tous les nombres premiers plus petits qu'un entier naturel N prédé ni.
ÉNONCÉ
À l'aide du crible d'Eratosthène, déterminer tous les nombres premiers inférieurs à 100.
ETAPE 1
Écrire la liste de tous les nombres inférieurs à N
On dresse, sous forme de tableau par exemple, la liste de tous les nombres inférieurs à N.
APPLICATION
On dresse la liste de tous les entiers inférieurs ou égaux à 100.
ETAPE 2
Éliminer 1
1 n'est pas un nombre premier, on le barre.
APPLICATION
On barre le 1 qui n'est pas un nombre premier.
Kartable.fr 1/4 Le crible d'Érathostène
Chapitre 3 Terminale S
Les nombres premiers Le crible d'Érathostène Mathématiques
ETAPE 3
Entourer 2 et éliminer les multiples de 2
2 est le premier nombre premier, on l'entoure.
Tous les multiples de 2 ne peuvent donc pas être premiers, on les barre.
APPLICATION
On entoure le 2 et on barre les multiples de 2.
ETAPE 4
Entourer 3 et éliminer les multiples de 3
Dans le tableau, on sélectionne le premier nombre suivant qui n'a pas été barré. Ce nombre est premier. Ici, 3 est le nombre
premier suivant, on l'entoure.
Tous les multiples de 3 ne peuvent donc pas être premiers, on les barre.
APPLICATION
On entoure le 3 et on barre les multiples de 3.
Kartable.fr 2/4 Le crible d'Érathostène
Chapitre 3 Terminale S
Les nombres premiers Le crible d'Érathostène Mathématiques
ETAPE 5
Entourer 5 et éliminer les multiples de 5
Dans le tableau, on sélectionne le premier nombre suivant qui n'a pas été barré. Ce nombre est premier. Ici, 5 est le nombre
premier suivant, on l'entoure.
Tous les multiples de 5 ne peuvent donc pas être premiers, on les barre.
APPLICATION
À l'aide de la liste, le nombre premier suivant est le 5. On l'entoure et on barre les multiples de 5.
ETAPE 6
⎯⎯
⎯
Renouveler le procédé jusqu'à la partie entière de √N
On réitère le procédé avec tous les nombres premiers inférieurs ou égaux à √⎯⎯N⎯ .
APPLICATION
À l'aide de la liste, le nombre premier suivant est le 7. On l'entoure et on barre les multiples de 7.
Ensuite le nombre premier suivant est le 11. Or 11 > √⎯100
⎯⎯⎯⎯⎯.
Donc on s'arrête là.
Kartable.fr 3/4 Le crible d'Érathostène
Chapitre 3 Terminale S
Les nombres premiers Le crible d'Érathostène Mathématiques
ETAPE 7
Conclure
On conclut en donnant la liste des nombres non barrés de la liste : ce sont les nombres premiers inférieurs à N.
APPLICATION
Les nombres premiers inférieurs à 100 sont donc :
2 − 3 − 5 − 7 − 11 − 13 − 17 − 19 − 23 − 29 − 31 − 37 − 41 −
43 − 47 − 53 − 59 − 61 − 67 − 71 − 73 − 79 − 83 − 89 − 97
Kartable.fr 4/4 Le crible d'Érathostène
Chapitre 3 Terminale S
Les nombres premiers Recherche des diviseurs d'un nombre grâce à sa Mathématiques
décomposition en produit de nombres premiers
SITUATION
A n de déterminer tous les diviseurs d'un entier n, on le décompose en produit de facteurs premiers.
ÉNONCÉ
Rechercher tous les diviseurs de 120.
ETAPE 1
Décomposer l'entier en produit de facteurs premiers
On décompose n en produit de facteurs premiers.
APPLICATION
La décomposition de 120 en produit de facteurs premiers est :
120 = 23 × 3 × 5
ETAPE 2
Lister tous les diviseurs
On liste tous les diviseurs de l'entier n. On pourra notamment s'aider d'un arbre.
APPLICATION
Les diviseurs de 120 seront donc tous de la forme : 2m × 3n × 5p avec :
m ∈ {0;1;2;3}, soit 4 choix pour m
n ∈ {0;1}, soit 2 choix pour n
p ∈ {0;1}, soit 2 choix pour p
A n de dresser la liste complète des diviseurs de 120, on dresse l'arbre ci-dessous :
ETAPE 3
Conclure
On conclut en donnant l'ensemble des diviseurs de n.
APPLICATION
On en conclut que l'ensemble des diviseurs de 120 est :
{1;2;3;4;5;6;8;10;12;15;20;24;30;40;60;120}
Kartable.fr 1/1 Recherche des diviseurs d'un nombre grâce à sa décomposition en produit de nombres premiers
Chapitre 3 Terminale S
Les nombres premiers Recherche du nombre de diviseurs d'un entier Mathématiques
naturel
n = ap × bq × cr possède (p + 1) × (q + 1) × (r + 1) diviseurs.
SITUATION
L'entier n dont la décomposition en facteurs premiers est
ÉNONCÉ
Déterminer le nombre de diviseurs de l'entier 720.
ETAPE 1
Décomposer n en produit de facteurs premiers
On décompose n en produit de facteurs premiers.
APPLICATION
La décomposition en produit de facteurs premiers de 720 est :
720 = 24 × 32 × 5
ETAPE 2
Réciter le cours
D'après le cours, on sait que le nombre de diviseurs d'un entier n est le produit des exposants apparaissant dans sa
décomposition en facteurs premiers, chacun augmenté de 1.
Ainsi l'entier n dont la décomposition en facteurs premiers est n = ap × bq × cr a (p + 1) × (q + 1) × (r + 1) diviseurs.
APPLICATION
Le nombre de diviseurs d'un entier n est le produit des puissances apparaissant dans sa décomposition en facteurs
premiers, chacune augmentée de 1.
ETAPE 3
...












