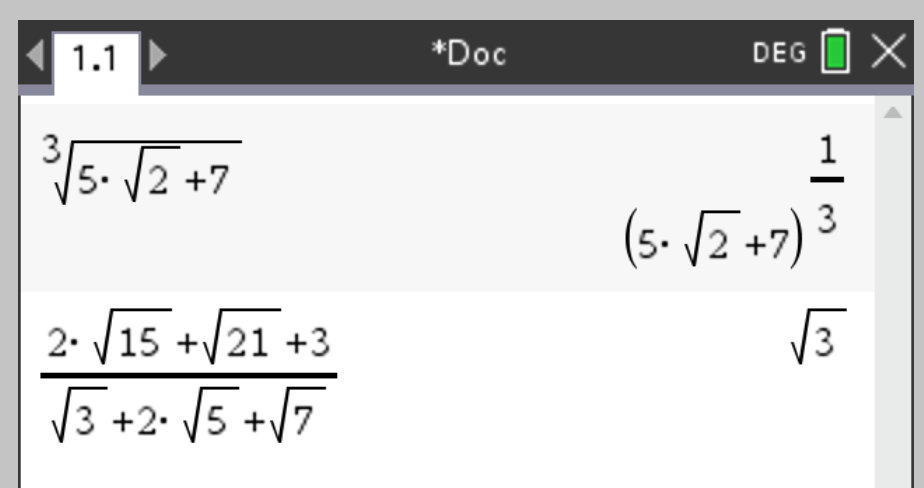Page 1 of 1
Simplifying radicals on TI-Nspire CAS - it is possible?

Posted:
11 Apr 2023, 10:12by bluestone
Нow to make the TI-Nspire CX CAS reduce variuos radical expressions (and whether it is capable of doing that, at all)?
like that

or more simple

I’m not talking about quite simple examples like

,

, but those where a bit more complex transformations are needed.
Тo make more sense of what it's about, here are examples done with other calculators:


Re: Simplifying radicals on TI-Nspire CAS - it is possible?

Posted:
11 Apr 2023, 12:55by Adriweb
Simplifications are automatic. So, whenever it can, it will do it.
For instance, it works fine on your first example, but can't simplify the 2nd one :
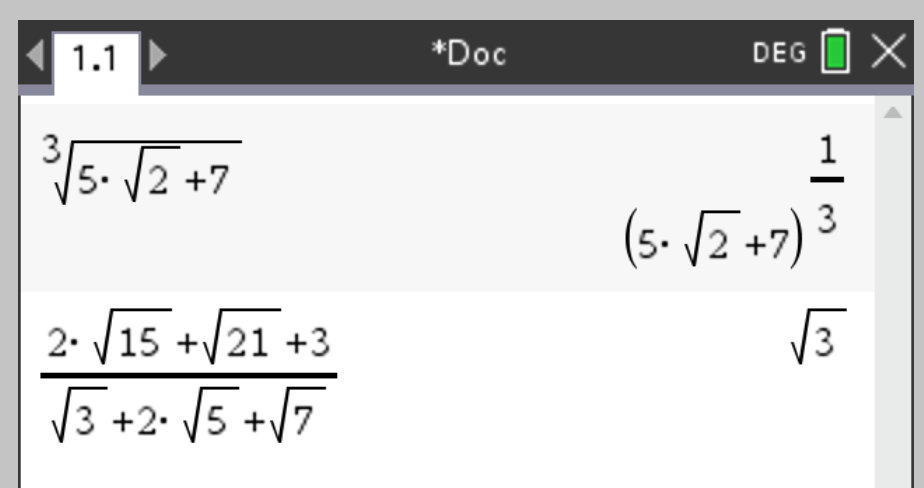
Re: Simplifying radicals on TI-Nspire CAS - it is possible?

Posted:
12 Apr 2023, 08:04by bluestone
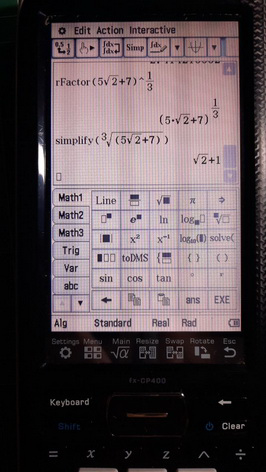
And then it turns out that the CP400 has more advanced CAS if it can do that?
Re: Simplifying radicals on TI-Nspire CAS - it is possible?

Posted:
12 Apr 2023, 08:11by Adriweb
Each CAS has their own advantages and drawbacks.
At least on the Nspire you can install third party CAS engines like KhiCAS (xcas, which is what the HP Prime has)
Re: Simplifying radicals on TI-Nspire CAS - it is possible?

Posted:
15 Apr 2023, 11:52by Hisham
In some cases it's possible to simplify nested (cubic) radicals. Let's suppose we have (m+n∙sqrt(p))^(1/3). The radicand should be of the type: (a+sqrt(b))^3 = a^3 + 3ab + (3a^2 + b)∙sqrt(b), that is m = (a^3 + 3ab) and n∙sqrt(p) = (3a^2 + b)∙sqrt(b). To be able to say that b=p (the radical part is not univocally determined), we'll need to look at the various "representations" of the radical and see if there is one where (n-p)/3 is a perfect square.
In such a case, we'll have a=sqrt((n-p)/3) and b=p, hence (m+n∙sqrt(p))^(1/3) = a+sqrt(b).
Example: (7+5∙sqrt(2)) = (a+sqrt(b))^3, where (a^3 + 3ab)=7 and a=sqrt((5-2)/3)=1 (b=p=2). Thus we get (7+5∙sqrt(2))^(1/3) = 1+sqrt(2).
This procedure could be "algorithmized" (i.e. through a system) for the TI-Nspire (with TI-Basic or Python) but it does not work in all cases (generally Landau's algorithm is used for the CAS calc).
Re: Simplifying radicals on TI-Nspire CAS - it is possible?

Posted:
15 Apr 2023, 12:04by Adriweb
Wolfram Alpha can give you the steps for this, too, but anyway


Re: Simplifying radicals on TI-Nspire CAS - it is possible?

Posted:
15 Apr 2023, 19:52by parisse
This is not the right way to simplify roots. The right way here is to factor x^3-(5*sqrt(2)+7) over Q[sqrt(2)], and to do that multiply by the conjugate, this gives x^6-14*x^3-1, factor it over the integers, you get 2 factors (x^2-2*x-1)*(x^4+2*x^3+5*x^2-2*x+1), then select the right one. If the polynomial is irreducible over the integers, then it can not be simplified (in that case the algebraic extension is of order 6).
Note that the general tool for something more complicated than sqrt is the resultant.
r:=resultant(x^3-(5y+7),y^2-2,y);
factor(r);
(you can run these commands with KhiCAS on compatible calculators, and on the Prime)


 ,
,  , but those where a bit more complex transformations are needed.
, but those where a bit more complex transformations are needed.